Ouroboros Phalanx - Breaking Grinding Incentives

Abstract

We propose an extension to Ouroboros Praos, called Ouroboros Phalanx. The name derives from the Phalanx, an Ancient Greek military formation where soldiers stood in tightly packed units, shielding one another to form a nearly impenetrable defense. Just as the phalanx multiplied the strength of individual soldiers through coordination, this protocol enhances Cardano’s consensus by reinforcing its resistance to adversarial attacks.

At its core, Phalanx Protocol strengthens the VRF-based randomness generation sub-protocol that underpins leader election. It introduces an additional cryptographic primitive that is lightweight for honest participants yet computationally expensive for adversaries seeking to bias slot leader distributions. This design does not eliminate grinding attacks outright but makes them economically infeasible at scale.

By addressing both CPS-0021: Randomness Manipulation and CPS-0017: Settlement Speed, Phalanx achieves two goals simultaneously:

• It raises the cost of grinding attacks by a factor of roughly 10¹⁰.
• It reduces settlement time by approximately 20–30% compared to unmodified Praos, without compromising security.

Ouroboros Phalanx therefore represents a complementary advancement: reinforcing Cardano’s consensus security while improving performance, and ensuring the network remains robust against future adversarial strategies.

Motivation: why is this CIP necessary?

This proposal strengthens Cardano’s consensus protocol (Ouroboros Praos) against a class of attacks known as grinding attacks. These attacks allow adversaries to bias the randomness used in block leader elections in their favor, statistically slowing down settlement times and thys weakening the effectivness of Praos.

The improvement introduces an additional computation step that is lightweight for honest participants but significantly more expensive for attackers, making grinding attacks economically infeasible.

Recommended Configuration

As an initial configuration, we recommend 12 hours of cumulative and distributed execution of this cryptographic primitive per epoch on standard CPU architectures.

• The epoch is divided into 1-hour intervals.
• The first leader of each interval must produce the corresponding proof.
• For any individual node, this requirement represents roughly 527 seconds (≈10 minutes) of computation.

The algorithm is designed so that with 128-bit confidence, all required proofs will be produced on time by the end of each epoch.

Security Improvements

The proposal increases substantially the computational cost of a grinding attack by a factor of approximately 10¹⁰ compared to the current situation.

To maintain this level of security over time:

• Governance may choose to increase the 12-hour budget as the cost of computation decreases.
• Execution could migrate to ASIC-based architectures, preserving the same budget while maintaining security guarantees, and later increasing the budget further.

Beyond parameter updates, adoption of this proposal would necessarily require a hard fork, since it modifies the consensus protocol in two fundamental ways:

1. The randomness for slot distribution is extended from 1 epoch to 2 epochs. At the start of epoch e, the snapshot of the stake distribution will be taken at the end of epoch e−2, rather than at the end of epoch e−1 as in Praos today.
2. The general method of generating slot leader distributions is changed, making leader election more resilient to adversarial bias.

Consensus Performance

This proposal is not only about security, but also about consensus performance.

In Praos, because grinding allows adversaries to choose among multiple possible slot leader distributions, the probability of “bad events” (such as rollbacks or settlement failures) is statistically amplified compared to the honest model.

• If a bad event occurs with probability $`\varepsilon`$ under unbiased randomness,
• An adversary able to try $`R`$ independent randomness candidates can increase the likelihood of that event up to $`R \cdot \varepsilon`$ (by the union bound).

This translates into slower settlement and weaker guarantees for the network as a whole. By substantially reducing $`R`$ compared to Praos, we limit the impact of grinding attacks and therefore improve settlement. In fact, the recommended configuration reduces settlement time by approximately 20–30% while maintaining equivalent security.

Relationship to Peras

Ouroboros Peras is a recent extension of Praos designed to accelerate settlement.

• Instead of waiting for the traditional 2160-block window (around 5 days) to guarantee finality, Peras introduces stake-weighted voting and certified blocks.
• Randomly chosen committees of stake pool operators can “vote” on blocks, and when enough votes are collected, the block receives a certificate.
• Certified blocks are treated as more important in the chain, which enables settlement in just 1–2 minutes.

Peras is fully compatible with Praos:

• When enough committee members participate, it achieves rapid settlement.
• When they do not (e.g., if too many operators are offline), Peras gracefully falls back to Praos. Peras would only fall back to Praos if there were massive network disruption or an attack by a 25% adversary.

In these fallback situations, the network still relies on Praos’ guarantees—precisely where Phalanx becomes relevant as a complementary defense layer. Phalanx ensures that even when Peras cannot certify blocks, the protocol still benefits from:

• Stronger protection against grinding attacks, and
• Faster settlement compared to unmodified Praos.

Together, they form a complementary pair:

• Peras provides speed when conditions are favorable.
• Phalanx ensures resilience and strong security guarantees in all cases.

Technical Depth

The remainder of this document provides the full technical specification for node implementors and researchers. Because Cardano’s security is grounded in cryptography, probability, and statistical guarantees, understanding the full details of this proposal requires technical knowledge in these areas. The complete specification is therefore dense: it describes mathematical models, cryptographic primitives, and rigorous proofs to ensure the system can be trusted at scale. Readers interested only in the high-level motivation and community impact may stop here.

Please refer to the CPD "Ouroboros Randomness Generation Sub-Protocol – The Coin-Flipping Problem" for a detailed understanding of randomness generation, leader election in Praos, and the coin-flipping dilemma in consensus protocols. Moving forward, we will dive into the core details, assuming you have the relevant background to understand the proposal.

Specification

The core principle of the proposed protocol change is to substantially escalate the computational cost of each grinding attempt for an adversary. To achieve this, every honest participant is required to perform a designated computation for each block they produce over an epoch (432,000 slots - 5 days) - note that this computation can be preprocessed locally at the beginning of the epoch. Consequently, an adversary attempting a grinding attack must recompute these operations for every single attempt, while being constrained by the grinding window, which dramatically increases the resource expenditure. By enforcing this computational burden, we drastically reduce the feasible number of grinding attempts an adversary with a fixed resource budget can execute, making randomness manipulation more expensive and significantly less practical.

1. High-Level Overview

1.1. Changes Relative to Praos

In Phalanx , the randomness generation and leader election flows are modified as follows:

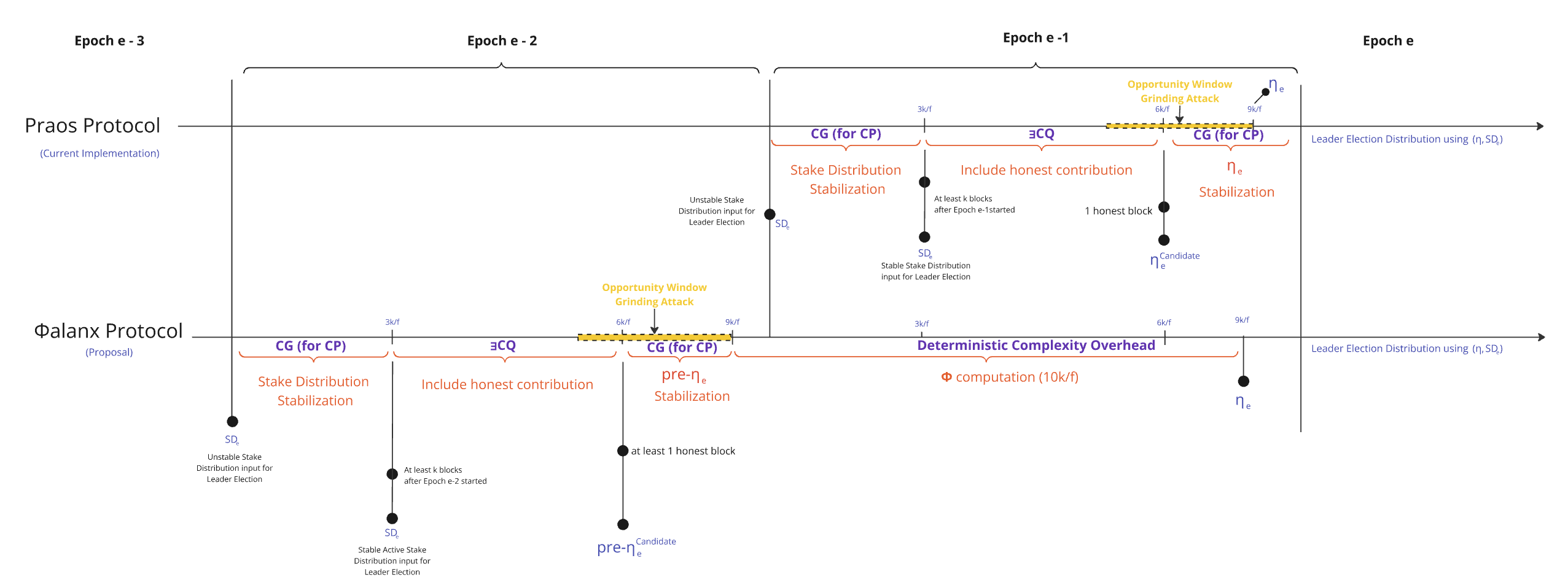
1. The stake distribution stabilization phase is shifted back by one epoch : The active stake distribution $`\mathbf{SD}_e`$ used for leader election is now derived from the end of $epoch_\text{e-3}$ instead of $epoch_\text{e-2}$ as in the original Praos protocol.
2. The honest contribution inclusion phase, which originally resulted in a ηₑ candidate, is also shifted back by one epoch, aligning with the adjusted stake distribution stabilization. This value is now referred to as the pre-ηₑ candidate, signifying its role as an intermediate randomness nonce in the sub-protocol.
3. The pre-ηₑ candidate, once stabilized (after $`3 \cdot \frac{k}{f}`$), undergoes a sequence of incremental operations using a new deterministic cryptographic primitive Φ (Phi). This sequence spans a full epoch size, specifically during the interval:$`\left[\frac{9k}{f} \cdot \text{epoch}_{e-2}, \frac{9k}{f} \cdot \text{epoch}_{e-1}\right)`$.
4. The final ηₑ (eta nonce), resulting from the Φ computation, completely determined by the prior stabilized pre-seed pre-ηₑ, does not need stabilization and is availablea a whole $`\frac{k}{f}`$ slots before the start of $`\text{epoch}_e`$ .

1.2. Inputs & Outputs

The Randomness Generation sub-protocol pipelines two parallel streams η stream and Φ Stream, which synchronize at $`9 \cdot \frac{k}{f}`$ at each epoch :

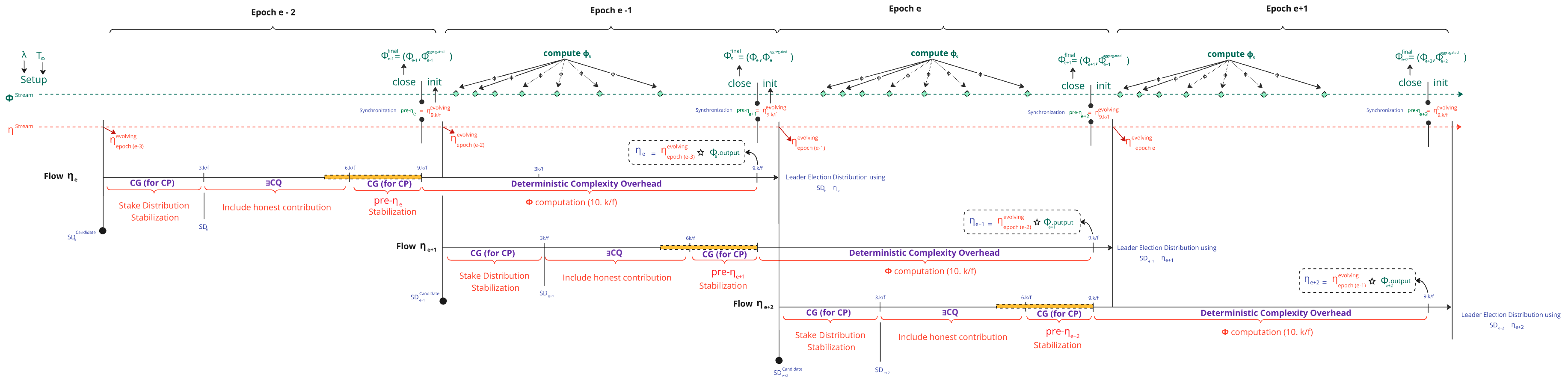
1.2.1. The η stream

• Already present in Praos and retained in Phalanx
• Updated with every block produced in the blockchain tree, a η stream captures intermediate values $`\eta^\text{evolving}_t`$ in the block headers, defined as follows:

$$\eta^{\text{evolving}}_{t+1} = \begin{cases} \eta^{\text{evolving}}_{t}\ \star\ \mathsf{VRF}^\text{Output}_\text{t+1} & \text{when BlockProduced}(t) \\ \eta^{\text{evolving}}_{t} & \text{otherwise.} \end{cases}$$ $$\text{BlockProduced}(t) = \begin{cases} \text{true} & \text{if a block is produced at time } t, \\ \text{false} & \text{otherwise.} \end{cases}$$

where
$`\text{ProtocolParameter}_\text{extraEntropy} `$	The evolving nonce is initialized using the extraEntropy field defined in the protocol parameters.
$`\mathsf{VRF}^\text{Output}_\text{i} `$	The VRF output generated by the $` \text{slot}_\text{i} `$ Leader and included in the block header
$a\ \star\ b$	The concatenation of $a$ and $b$ , followed by a BLAKE2b-256 hash computation.

1.2.2. The pre-ηₑ Synchronizations

• To generate $`\eta_\text{e}`$ for epoch $`e`$, the stream Φ Stream is reset with the value of η stream at $`t=9.\frac{k}{f}`$ at $epoch_{e-2}$
• This specific value of η stream is referred to as $`\text{pre-}\eta_e`$ and defined as :

$$\text{pre-}\eta_e= \eta^{evolving}_{9.\frac{k}{f}(epoch_{e-2})}$$

1.2.3. The Φ Stream

1.2.3.1. The Setup

The stream is bootstrapped by calling the parametrize function of the cryptographic primitive $`\Phi`$ with:

$$Φ.\text{Stream.State} \leftarrow \Phi.\text{parametrize}(\lambda, T_\Phi)$$

where :

• $`\lambda`$ is a security parameter for the cryptographic primitive $`\Phi`$.
• $`T_\Phi`$, a time-bound parameter representing the required computation $`\Phi`$ duration, independent of available computing power.
• Any change to these 2 parameters would require a decision through Cardano governance.
• $\Phi.\text{Stream.State}$ will contain derived configuration specific to the algorithm and the cryptographic primitive used.

1.2.3.2. The Lifecycle

It is reset at every pre-ηₑ synchronization point every $`10.\frac{k}{f}`$ slots :

$$Φ.\text{Stream.State} \leftarrow \Phi.\text{initialize}(Φ.\text{Configuration}, \text{pre-}\eta)$$

At each slot $t$, update the stream state by :

$$Φ.\text{Stream.State} \leftarrow \Phi.\text{tick}(Φ.\text{Stream.State, t})$$

A node must be able to determine, based on the current state, whether it should begin computing $\Phi$ iterations in order to provide a proof at its next scheduled leader slot (see Section "3.2.4.1. VDF integration" for details):

$$\{0,1\} \leftarrow \Phi.\text{shouldCompute}(Φ.\text{Stream.State, nextElectedSlot})$$

A node must be able to compute a specific chunk of the $`\Phi`$ iterations independently of any global state. The result is an attested output—a pair $`\phi_x =(\pi_x,\ o_x)`$ where :

• $`o_x`$ is the computed output for iteration $`x`$,
• $`\pi_x`$ is a cryptographic proof attesting that $`o_x`$ was correctly derived from the input according to the rules of $`\Phi`$.
• Since this operation may be long-lived, intermediate attested outputs should be persistable to disk, allowing the node to stop, resume, or cancel computation from the latest completed sub-computation.

A subset of block-producing slots must include in their block bodies a unique attested output $`\phi_x`$ with $`x \in \{1,\ \dots,\ i \}`$ denoting the iteration index within the $`\Phi`$ computation :

• Each attested output updates the stream state as follows:

$$\Phi.\text{StreamState} \leftarrow \Phi.\text{provideAttestedOutput}(\Phi.\text{StreamState},\ t,\ \phi_x)$$

• Each attested output must be verifiable both:
  • logically, to ensure it corresponds to the correct slot and index, and
  • cryptographically, to confirm that the computation was effectively executed

$$\{0,1\} \leftarrow \Phi.\text{verify}(\Phi.\text{StreamState},\ t,\ \phi_x)$$

At the synchronization point $`\text{pre-}\eta_{e+1}`$, the stream is closed providing $`\phi^{final}_e = (\phi_e,\ \phi^{aggregated}_e)`$ with the last attested output $`\phi_e\text{,}`$ along with an aggregated proof $`\phi^{final}_e`$. This aggregated proof fastens node synchronisation by allowing nodes to efficiently verify the final result without checking each individual $`\phi_x`$ produced during the computation phase :

$$\phi^{final}_e \leftarrow \Phi.\text{close}( \Phi.\text{StreamState})$$

1.2.4. The η Generations

• This is the final nonce $`\eta_\text{e}`$ used to determine participant eligibility during epoch $`e`$.
• It originates from the operation $`\star`$ with $`\phi^{\text{stream}}_{t}`$ at $`\text{pre-}\eta_\text{e+1}`$ synchronization and η stream $`\text{when } t = \text{end of epoch}_\text{e-3}`$ and the combination of the outputs $`\{o_i\}_{[1,i]}`$ using an aggregation function $`f_\text{agg}`$.

$$\eta_\text{e} = \eta^\text{evolving}_{epoch_\text{e-3}}\ \star\ f_\text{agg}(o_1, \dots, o_e) , \quad \text{when } t = \text{pre-}\eta_\text{e+1}\text{ synchronization }$$

2. The Φ Cryptographic Primitive

2.1. Expected Properties

The Φ cryptographic primitive is a critical component of the Phalanx protocol, designed to increase the computational cost of grinding attacks while remaining efficient for honest participants. To achieve this, Φ must adhere to a set of well-defined properties that ensure its security, efficiency, and practical usability within the Cardano ecosystem. These properties are outlined in the table below :

Property	Description
Functionality	Must be a well-defined mathematical function, ensuring a unique output for each given input (unlike proof-of-work, which allows multiple valid outputs).
Determinism	Must be fully deterministic, with the output entirely determined by the input, eliminating non-deterministic variations.
Efficient Verification	Must allow for fast and lightweight verification, enabling rapid validation of outputs with minimal computational overhead.
Compact Representation	Input and output sizes should be small enough to fit within a block, optimizing on-chain storage efficiency. Further reductions are desirable where feasible.
Lower Bound on Computation	Computational cost of evaluation should be well-characterized and predictable, with a lower bound that is difficult to surpass, ensuring adversaries cannot gain an unfair efficiency advantage.
Ease of Implementation & Maintenance	Should be simple to implement and maintain, ensuring long-term usability and minimizing technical debt.
Adaptive Security	Function and its parameters should be easily reconfigurable to accommodate evolving threats, such as advances in computational power or new cryptographic attacks.

2.2. Verifiable Delayed Functions (VDF)

Verifiable Delayed Functions (VDFs) are cryptographic primitives designed to take a certain amount of time to compute, regardless of how much computing resources are available. This delay is enforced by requiring a specific number of sequential steps that cannot be easily sped up through parallel processing. Once the computation is done, the result, $`y = g^{2^T}`$, comes with a proof, $`\pi`$, that can be checked quickly and efficiently by anyone. Importantly, for a given input, the output is always the same (deterministic function), ensuring consistency. They usually rely on repeatedly squaring numbers in a mathematical setting that prevents shortcuts and enables quick verification.

As one can see, VDFs present functionality, determinism, efficient verification and lower bound on computation. The compact representation depends on the chosen group as well as the instantiation, which we will tackle later on. The implementation and maintenance is straightforward as the output of a VDF is a simple exponentiation of a group element, only the square operation is needed to be implemented to compute it. As for the proof, this depends on the precise VDF instantiation. Finally, the system is "adaptively secure" as we can set up a group with high security to be reused for a whole epoch or more, and set the number of squaring, also called difficulty, depending on how much computation we want the nodes to perform.

Verifiable Delayed Functions were introduced by Boneh et al. [6] where the authors suggest several sequential functions combined with the use of proof systems in the incrementally verifiable computation framework (IVC) for viable proof generation and fast verification. VDF variants revolve around two primary SNARK-free designs: one from Pietrzak [36] and the second from Wesolowski [35]. They differ in the proof design.

In Wesolowski’s paper, the proof is defined as $g^{{2^T} /\ p}$ where $g$ is the challenge, $T$ the difficulty and $p$ is a prime number found by hashing the VDF input and output together.
The proof is thus a single group element that can be computed in at most $2\cdot T$ group operations and constant space, or $(1+1/s) \cdot T$ time where the number $s$ is both the number of processors and space while the verification takes $\text{log}_2 T$ scalar multiplications in $\mathbb{Z}/p$ and two small exponentiations in the group $\mathbb{G}$. The proving time can further be optimized to $O(T /\ \text{log}(T))$ group multiplications by reusing the evaluation intermediary results.
Wesolowski also presents aggregation and watermarking methods. The aggregation method does not consist in aggregating multiple proofs but computing a proof of several VDF challenges. This is done by batching all inputs and outputs together and creating a proof for this batched input. The watermarking is done by computing the VDF twice, once normally and another time on a combination of the challenger’s id and VDF input.

In Pietrzak’s paper, the proof is a tuple of group elements $\pi = \{x^{2^{T / 2^i}}\}$, of size logarithmic in $T$, that can be computed in $(1+2 /\sqrt{T})\cdot T$ time and can be optimized to $O(\sqrt{T} \cdot \text{log}_2 T)$ multiplications. The verification takes $2 \cdot \text{log}_2T$ small exponentiations. Subsequent work on Pietrzak’s paper shows how VDFs challenges can be structured in a Merkle tree to get a proof of the whole tree.

We will choose Wesolowski design over Pietrzark because of its space efficiency and possibility to aggregate proofs.

Specialized hardware such as ASICs can be used to evaluate VDF output much faster, up to a factor 5 in Chia's VDF project while Ethereum considers a factor 10. This, while unfortunate, is not prohibitive in our context as we only consider the use of VDFs for their computational cost. An attacker would still require a substantial budget to perform an anti-grinding attack in addition to purchasing at scale the specialized hardware that is not inexpensive nor readily available (Chia' ASICs can be purchased on a case per case basis for $1,000). We can also note that any solution would still be affected by hardware, like in the case of proof of works and hash farms.

2.3. Wesolowski's VDF

2.3.1. VDF Primitives

To define Wesolowski VDF construction, we first introduce a series of hash functions: $`\text{Hash}^{(n)}_\mathbb{N}`$, which samples random integers of $`n`$ bits, $`\text{Hash}^{(n)}_\text{prime}`$, which samples a random integer from the set of the first $`2^{2n}`$ prime numbers, and $`\text{Hash}_\mathbb{G}`$, which samples a random group element of the class group $`\mathbb{G}`$.

We define the interface of a Verifiable Delay Function as $`\texttt{VDF} = (\texttt{Setup},\ \texttt{Evalute},\ \texttt{Prove},\ \texttt{Verify})`$, and define its underlying functions based on class groups as follows:

• $`(\mathbb{G},\ \Delta,\ \cdot) \leftarrow \texttt{VDF.Setup}(\lambda,\ \Delta_{\text{challenge}})`$ Takes as input a security parameter $`\lambda \in \mathbb{N}`$ and a challenge discriminant $`\Delta_{\text{challenge}} \in \{0,1\}^*`$. This challenge discriminant acts as a source of public entropy used to deterministically derive the group discriminant $\Delta$, which defines a group of unknown order $\mathbb{G}$ along with its group operation $`\cdot`$. The use of a challenge ensures that the resulting group is unbiasable and unpredictable, preventing adversarial precomputation. We shall drop the group settings $`(\mathbb{G},\ \Delta,\ \cdot)`$ from further functions for readability. Internally, we expect the setup procedure to invoke the following sub-operations:

$$\Delta \leftarrow \texttt{VDF.CreateDiscriminant}(\lambda,\ \Delta_{\text{challenge}})$$ $$(\mathbb{G},\ \cdot) \leftarrow \texttt{VDF.DeriveClassGroup}(\lambda,\ \Delta)$$

• $`y \leftarrow \texttt{VDF.Evaluate}(\ x,\ I)`$ Given a challenge $`x \in \mathbb{G}`$ and a number of iterations $`I \in \mathbb{N}`$, computes the output $`y = x^{2^I}`$.

• $`\pi \leftarrow \texttt{VDF.Prove}(\ x,\ y,\ I)`$ Given a challenge and output $`(x,y) \in \mathbb{G}^2`$, computes the VDF proof as $`\pi = x^{2^I / p}`$ where $`p \leftarrow \text{Hash}^{(2 \lambda)}_\text{prime}(x \| y)`$ is sampled from the first $`2^{2 \lambda}`$ prime numbers.

• $`\{0,1\} \leftarrow \texttt{VDF.Verify}( \ x,\ y,\ I,\ \pi)`$ Returns 1 if $`\pi`$ successfully attests that $`y = x^{2^I}`$ with overwhelming probability, that is if $\pi^r \cdot x^p == y$ where $`p \leftarrow \text{Hash}^{(2 \lambda)}_\text{prime}(x \| y)`$ and $`r \leftarrow 2^I \text{mod}\ p`$. Returns 0 otherwise.

2.3.2. VDF Aggregation Primitives

In this section, we present a mechanism for producing a Wesolowski VDF aggregation proof. This construction enables efficient synchronization for network participants and may play a central role in deriving the final epoch nonce $`\eta_e`$. The aggregation mechanism has the following interface $`\texttt{VDF.Aggregation} = (\text{Init},\ \text{Update},\ \text{Prove},\ \text{Verify})`$ whose functions will be detailled afterwards. We assume that a class group $`\mathbb{G}`$ has already been set up, by $`(\mathbb{G},\ \Delta,\ \cdot) \leftarrow \texttt{VDF.Setup}(\lambda,\ \Delta_{\text{challenge}})`$.

N.B. We are showing here the core algorithms for simplicity and readability. In practice, we may use further techniques, for instance using an arbitrary byte and the epoch's number as personalization tags to ensure domain separation.

At the beginning of each epoch, we initialize the VDF accumulators' state that will be used to generate the VDF aggregation proof using $`\texttt{VDF.Aggregation.Init}`$.

Initialize accumulators	$`(\text{Acc}_x, \text{Acc}_y, \alpha) \leftarrow \texttt{VDF.Aggregation.Init}(\lambda, \text{pre-}\eta_e)`$
Input Parameters	$`\lambda \in \mathbb{N}`$ — Security parameter. $\text{pre-}\eta_e \in \{0,1\}^{256}$ — 256-bit pre-nonce entropy for epoch $e$.
Steps	Compute all VDF challenges: $`\forall i\ x_i \leftarrow \text{Hash}_\mathbb{G}(\text{pre-}\eta_e \|\|\ i) `$ Compute the initial aggregation nonce: $`\alpha \leftarrow \text{Hash}^{(\lambda)}_\mathbb{N}(x_1 \|\| \dots \|\| x_n) `$ Initializes the accumulators to the identity: $`(\text{Acc}_x,\ \text{Acc}_y) \leftarrow (1_\mathbb{G},\ 1_\mathbb{G})`$
Returned Output	$`(\text{Acc}_x,\ \text{Acc}_y,\ \alpha)`$ — Input and output accumulators and initial aggregation nonce.

Every time a VDF output is published on-chain, if no previous VDF outputs are missing, we shall update the accumulators' state using $`\texttt{VDF.Aggregation.Update}`$.

Update accumulators	$`(\text{Acc}_x, \text{Acc}_y, \alpha) \leftarrow \texttt{VDF.Aggregation.Update}(\lambda, (x_i, y_i),\ (\text{Acc}_x,\ \text{Acc}_y,\ \alpha))`$
Input Parameters	$`\lambda \in \mathbb{N}`$ — Security parameter. $`(x_i,\ y_i)`$ — Pair of VDF input and output for current interval. $`(\text{Acc}_x,\ \text{Acc}_y,\ \alpha)`$ — Accumulators' state.
Steps	Compute the aggregation nonce: $`\alpha \leftarrow \text{Hash}^{(\lambda)}_\mathbb{N}(\alpha\ \|\|\ y_i) `$ Update the accumulators: $`(\text{Acc}_x, \text{Acc}_y) \leftarrow (\text{Acc}_x \cdot x_i^\alpha,\ \text{Acc}_y \cdot y_i^\alpha)`$
Returned Output	$`(\text{Acc}_x,\ \text{Acc}_y,\ \alpha)`$ — Updated accumulator's state.

Once all VDF outputs have been generated and the accumulators updated, we can generate the VDF aggregation proof $`\pi`$ using $`\texttt{VDF.Aggregation.Prove}`$.

Prove accumulators	$`\pi \leftarrow \texttt{VDF.Aggregation.Prove}(\ (\text{Acc}_x,\ \text{Acc}_y,\ \_\alpha),\ I)`$
Input Parameters	$`(\text{Acc}_x,\ \text{Acc}_y,\ \alpha)`$ — Accumulators' state. $`I \in \mathbb{N}`$ — Per-interval iteration count for the VDF.
Steps	Compute the accumulator proof as a VDF proof: $`\pi \leftarrow \texttt{VDF.Prove}(\text{Acc}_x,\ \text{Acc}_y,\ I)`$
Returned Output	$`\pi`$ — Aggregated proof.

The VDF aggregation proof $`\pi`$ can then be efficiently be verified using $`\texttt{VDF.Aggregation.Verify}`$.

Verify accumulators	$`\{0,1\} \leftarrow \texttt{VDF.Aggregation.Verify}(\ (\text{Acc}_x,\ \text{Acc}_y,\ \_\alpha),\ I,\ \pi)`$
Input Parameters	$`(\text{Acc}_x,\ \text{Acc}_y,\ \alpha)`$ — Accumulators' state. $`I \in \mathbb{N}`$ — Per-interval iteration count for the VDF. $`\pi \in \mathbb{G}`$ — Aggregated VDF proof.
Steps	Verfy the accumulators' proof: $`b \leftarrow \texttt{VDF.Verify}(\text{Acc}_x,\ \text{Acc}_y,\ I,\ \pi)`$
Returned Output	$`b`$ — Verification bit.

3. Φ Stream Specification

We previously outlined the purpose of the Phalanx sub-protocol and introduced the cryptographic primitive underpinning its security guarantees. In this section, we provide a precise technical specification of the protocol, focusing on how the $`\Phi`$ iterations are distributed and how Wesolowski’s Verifiable Delay Function (VDF) is integrated into the process.

3.1. Distribution of Φ Iterations

As previously mentioned, Φ Stream is divided into epoch-sized lifecycle segments. Each segment begins with an initialize function, ends with a close function, and is immediately followed by the start of a new segment.

We further partition this segment into intervals, each large enough to guarantee (with 128-bit confidence) that at least one block will be produced within it. This corresponds to 3435 slots per interval. For simplicity, we round this to 3600 slots (~1 hour), resulting in exactly 120 intervals per segment, which conveniently aligns with the 120 hours in five days.

🔍 How 128-bit Confidence gives 3435 Slots ?

📦 Guaranteeing Honest Block Inclusion with 128-bit Confidence in our context

We want to make sure that, in any given interval of $N$ slots, there's at least one honest block produced — with a failure probability of at most $2^{-128}$ (which is a standard for cryptographic security).

It is also important to note that we are operating in a context where fork-related concerns can be safely abstracted away. In particular, if an adversary were to attempt a private chain attack and succeed, it would imply that their chain is denser and that the proof of $\Phi$ computation is valid. In this setting, forks do not undermine security—they actually improve the probability of having at least one valid computation published within the interval.

This means: $`\Pr(\text{at least one honest block in } N \text{ slots}) \geq 1 - 2^{-128}`$

🎲 Step 1 — What’s the chance of not getting an honest block?

Each slot gives honest participants a chance to be selected as leader.

Let:

• $f = 0.05$ → probability a slot is active
• $\sigma = 0.51$ → at least 51% of stake is honest

Then the chance that no honest party is selected in a slot is: $`(1 - f) + f \cdot(1-\sigma) = 0.95 + 0.05 \cdot (1-0.51) \approx 0.97449`$

So, the chance that at least one honest party is selected in a slot is: $`p_h = 1 - 0.97449 = 0.0255`$

This means that each slot has a 2.584% chance of having an honest leader.

📐 Step 2 — What about across $N$ slots?

The chance that no honest block is produced in $N$ consecutive slots is: $`(1 - p_h)^N`$

We want this to be less than or equal to $2^{-128}$, so: $(1 - p_h)^N \leq 2^{-128}$

✏️ Step 3 — Solve for $N$

Take log base 2 of both sides:

$\log_2((1 - p_h)^N) \leq \log_2(2^{-128})$

$N \cdot \log_2(1 - p_h) \leq -128$

$N \geq \frac{-128}{\log_2(1 - p_h)}$

Now plug in:

$`\log_2(1 - 0.0255) = \log_2(0.97449) \approx -0.03726`$

$`N \geq \lceil \frac{128}{0.03726} \rceil = 3435`$

To guarantee with 128-bit confidence that an interval contains at least one honest block, the interval must be at least 3435 slots long.

This ensures security even if up to 49% of stake is adversarial.

---

This structure can be illustrated as follows:

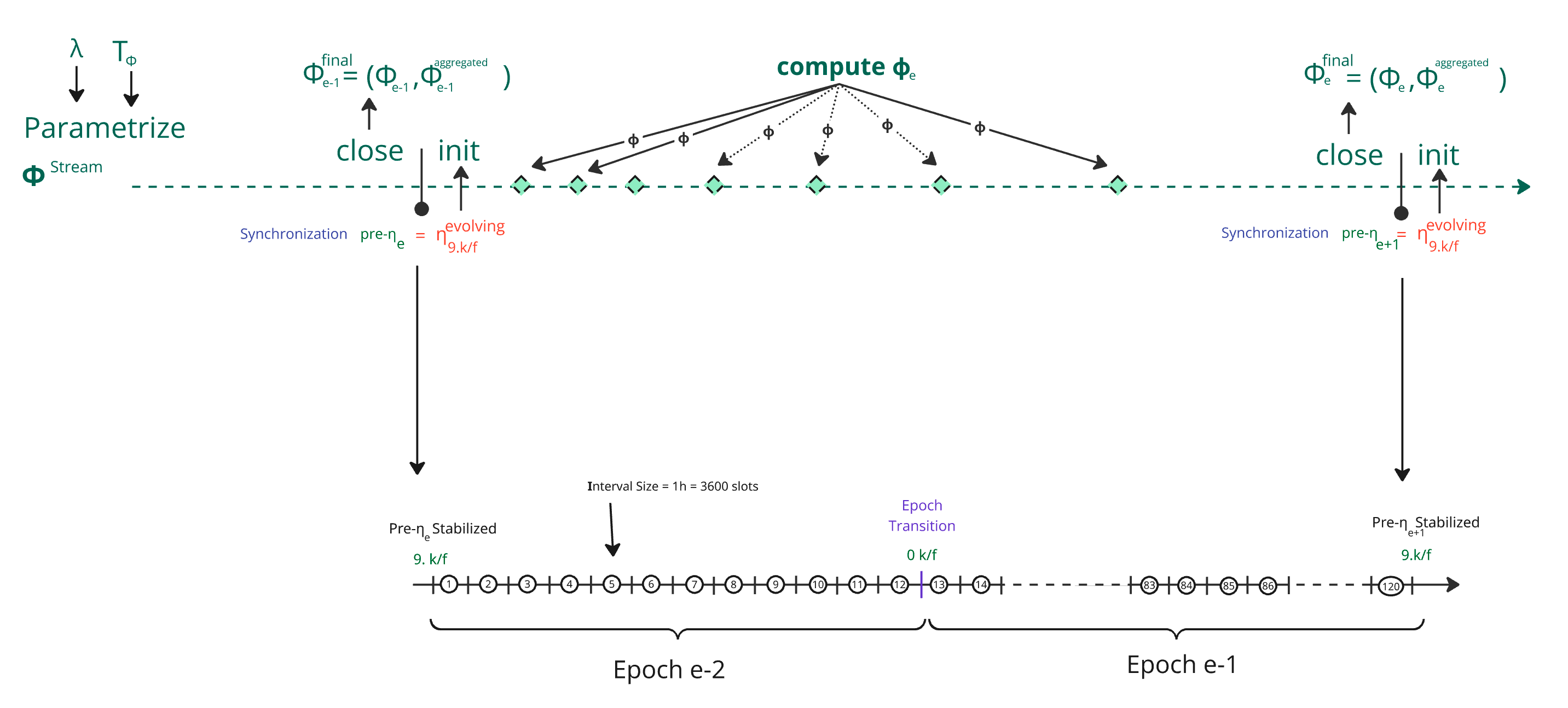
As previously described, we configure the stream using two key parameters, most notably the total computational budget $`T_\Phi`$. This value defines the total amount of work we require SPOs to collectively perform.

We split $`T_\Phi`$ into discrete iterations, each with the following properties:

• Iterations are fully independent and can be computed in parallel.
• Slot leaders are responsible for submitting a proof of computation for the specific iteration assigned to them.
• These computations are fully decoupled, there is no requirement to wait for previous iterations, enabling input precomputation and reducing latency.
• All iterations must eventually be completed, and an additional and final iteration is used to aggregating all outputs along with a corresponding proof.
• The iterations are then used to compute the epoch randomness $\eta_e$.

Each iteration is mapped to a specific interval, with the following constraints:

• The first interval is intentionally left without an assigned iteration, giving slot leaders time to compute the first output for interval #2 and allowing precomputation of the challenges.
• Each interval must be longer than the time required to compute a single iteration (i.e., the iteration duration must be less than one hour).
• The first slot leader to produce a block within an interval is responsible for submitting the corresponding attested output.

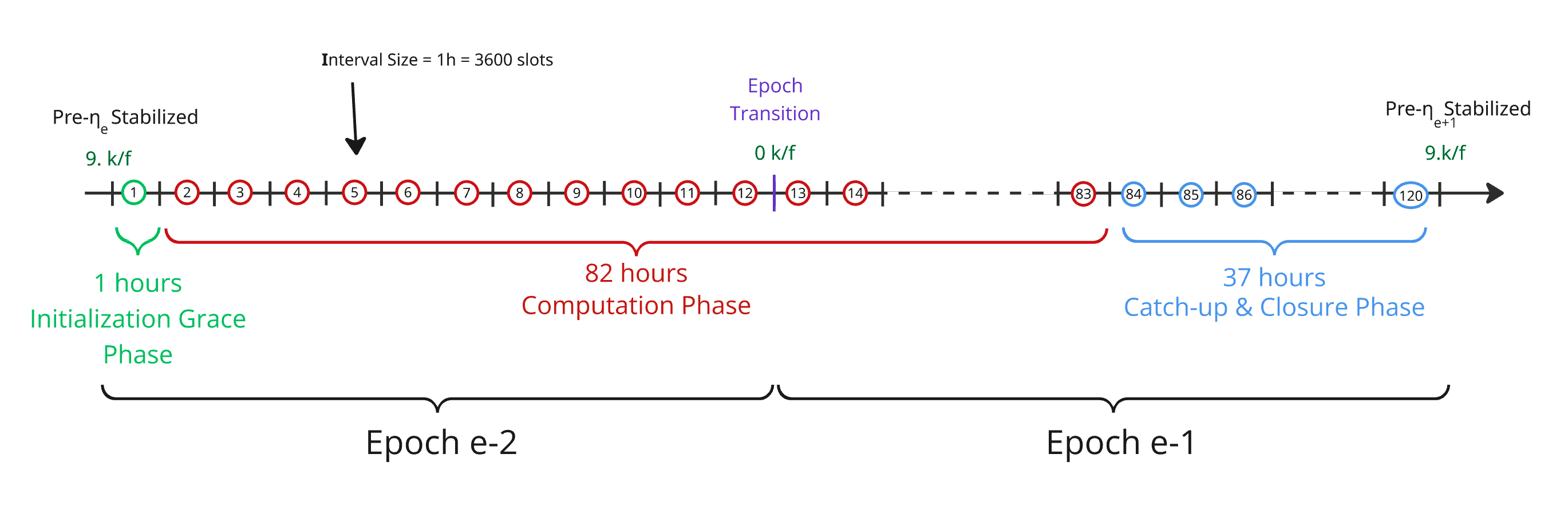
At first glance, we could divide $`T_\Phi`$ evenly across the 120 intervals. However, to ensure resilience, the protocol must remain robust even in extreme scenarios—such as a global outage causing 36 hours of consecutive downtime (30% of an epoch). This scenario is detailed in the Cardano Disaster Recovery Plan.

A global outage implies a sequence of blockless intervals. To tolerate such conditions, the protocol must be able to handle up to 36 intervals without block production. To address this, we introduce a catch-up mechanism:

• We reserve the final 36 intervals of the segment specifically for recovering any missing attested outputs.
• These missing outputs must be submitted in order, according to their original indices, ensuring deterministic reconstruction of the full computation stream.

We define 4 sequential phases in the stream lifecycle:

• 🟧 Parametrization Phase : The stream is configured but not yet active. Parameters such as $`\lambda`$ (computation hardness) and $`\#\text{iterations}_\phi`$ (number of iterations) are established during this phase.

• 🟩 Initialization Grace Phase: The stream is activated, and Stake Pool Operators (SPOs) are given a grace period to begin the first iteration of the computation.

• 🟥 Computation Phase: During this phase, the protocol expects attested outputs to be published on-chain. It consists of 82 computation iterations, each producing an intermediate output that contributes to the final result.

• 🟦 Catch-up & Closure Phase:

  • A bounded recovery window that allows SPOs to submit any missing attested outputs, ensuring the completeness of the computation prior to finalization.
  • A final dedicated interval to compute the aggregation of all previous outputs and derive the epoch’s final randomness $`\eta_e`$. This phase seals the stream and concludes a lifecycle.

The diagram below illustrates how the lifecycle segment is structured:

3.2. The State Machine

3.2.1. Diagram Overview

The figure below presents the state transition diagram for the Phalanx computation stream. Each node represents a distinct state in the lifecycle of the stream, and the arrows indicate transitions triggered by Tick events. These transitions are guarded by boolean predicates evaluated at each slot (e.g., isWithinComputationPhase, isWithinCurrentInterval).

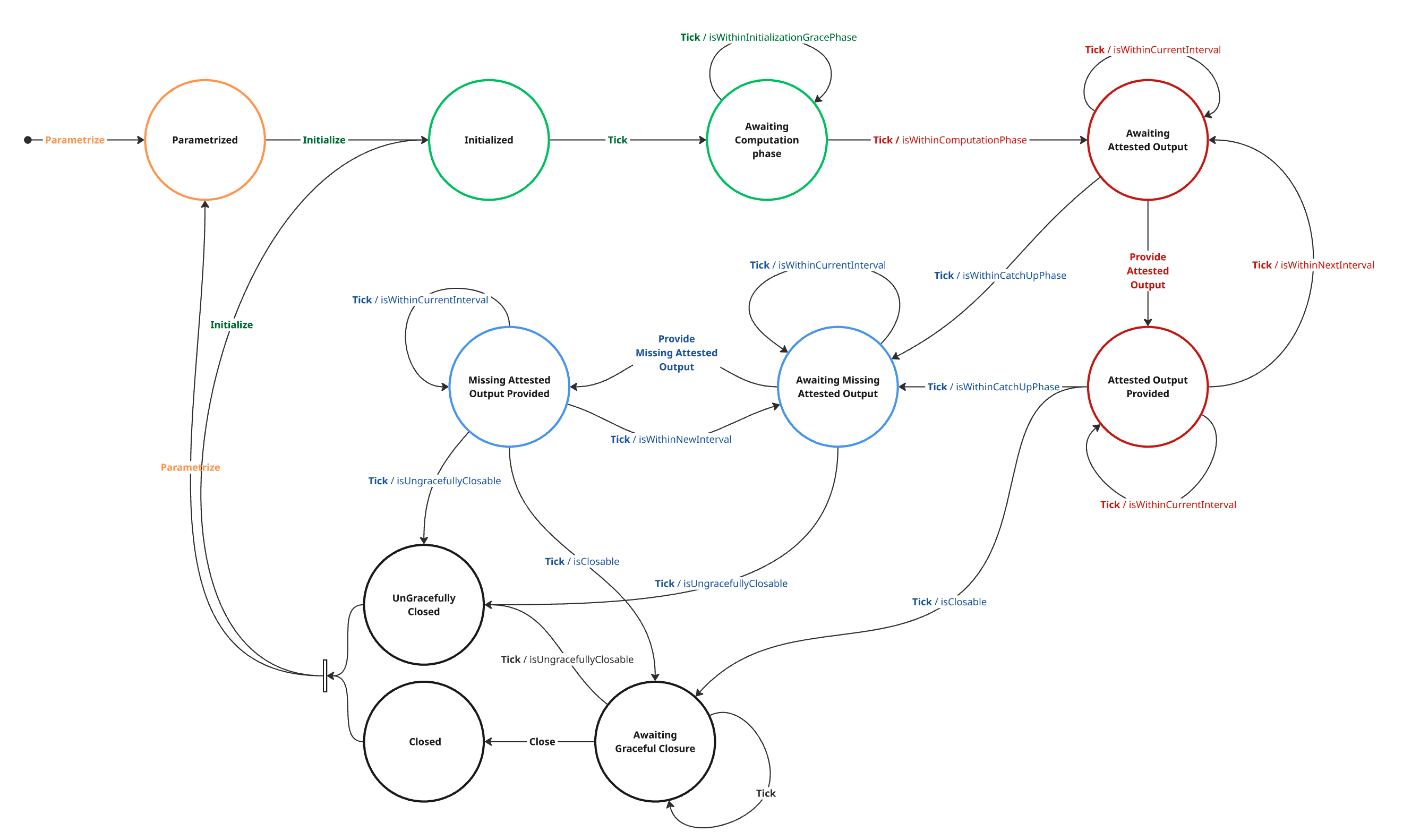
In the following sections, we provide a detailed breakdown of each phase of the state machine, specifying its purpose, entry conditions, timing constraints, and transitions.

3.2.2. 🟧 Parametrization Phase

At the setup of $`\phi^{stream}`$, the total number of VDF iterations is derived from the time-bound parameter $`T_\Phi`$, using a reference hardware profile that reflects the minimal computational capacity expected of SPOs. While this derivation may not be fully automatable in practice, we include it here to clarify how time constraints are mapped to iteration counts during configuration.

Importantly, this parametrization phase occurs only once, either during the initial bootstrap of the stream or following a transition from the Closed to Initialized state.

Parametrized	$`\Phi.\text{Stream.State} \in \texttt{Parametrized} : \left\{ {securityParameter} \in \mathbb{N},\quad I \in \mathbb{N} \right\}`$
Fields	$`\text{securityParameter} \in \mathbb{N}`$ — The security parameter, defining the size (in bits) of the VDF discriminant. $`I \in \mathbb{N}`$ — The per-interval VDF iteration count, computed from $`T_\Phi`$ and evenly distributed across 82 computation intervals.

parametrize	$`\Phi.\text{Stream.State} \leftarrow \Phi.\text{parametrize}(\lambda,\ T_\Phi)`$
Input Parameters	$`\lambda \in \mathbb{N}`$ — Security parameter, defines the size (in bits) of the VDF discriminant. $`T_\Phi \in \mathbb{N}`$ — Time budget in seconds, representing the total computation time under reference hardware.
Derivation Logic	$`\#\text{Iterations}_\Phi \leftarrow \texttt{VDF}.\texttt{IterationsFromDuration}(T_\Phi)`$ $`\#\text{Iterations}_\phi \leftarrow \left\lfloor \frac{\#\text{Iterations}_\Phi}{82} \right\rfloor`$
Returned State	$`\texttt{Parametrized} \left\{ \text{securityParameter} \leftarrowtail \lambda,\quad I \leftarrowtail \#\text{Iterations}_\phi \right\}`$

3.2.3. 🟩 Initialization Grace Phase

Initialization occurs at every pre-ηₑ synchronization point, followed by an Initialization Grace period during which the protocol waits long enough for the first iteration to be computed and its proof to be included within the first computation interval. This process recurs every $`10 \cdot \frac{k}{f}`$ slots.

3.2.3.1. Initialize Command

We show here how to initialize the class-group based VDF algorithm when generating a group for each different epoch. Were we to use the same group for many, if not all, epochs, we would run these steps in the Parametrization phase and change the discriminant seed $`\Delta_{\text{challenge}}`$ accordingly, e.g. if we use the same group forever we could use $`\Delta_{\text{challenge}} \leftarrow \text{Hash}(\text{bin}(\text{``IOHKPhalanx2025"}))`$.

Initialized

$`\Phi.\text{Stream.State} \in \texttt{Initialized} : \left\{ \text{parametrized} \in \texttt{Parametrized},\ \text{group} \in \mathbb{G},\ \text{discriminant} \in \mathbb{Z},\ \text{operation} : \mathbb{G} \times \mathbb{G} \to \mathbb{G} \right\}`$

Fields

$\text{parametrized} \in \texttt{Parametrized}$ — Reference to the prior configuration (security parameter and iteration count). $\text{group} \in \mathbb{G}$ — VDF group used for exponentiation. $\text{discriminant} \in \mathbb{Z}$ — Epoch-specific VDF discriminant. $\text{operation} : \mathbb{G} \times \mathbb{G} \to \mathbb{G}$ — Group operation used for VDF evaluation (e.g., modular exponentiation). $\text{epochId}_e \in \mathbb{N}$ — Numerical identifier for epoch $e$. $\text{pre-}\eta_e \in \{0,1\}^{256}$ — 256-bit pre-nonce entropy for epoch $e$.

initialize	$\Phi.\text{Stream.State} \leftarrow \Phi.\text{Initialize}(\text{parametrizedState},\ \text{epochId}_e,\ \text{pre-}\eta_e)$
Input Parameters	$\text{parametrizedState} = (\lambda,\ I) \in \texttt{Parametrized}$ — Configuration from the prior Parametrized state. $\text{epochId}_e \in \mathbb{N}$ — Numerical identifier for epoch $e$. $\text{pre-}\eta_e \in \{0,1\}^{256}$ — 256-bit pre-nonce entropy for epoch $e$.
Derivation Logic	$`\Delta_{\text{challenge}} \leftarrow \text{Hash}(\text{bin}(\text{epochId}_e) \ \|\ \text{pre-}\eta_e)`$ $`(\mathbb{G},\ \Delta,\ \cdot) \leftarrow \texttt{VDF.Setup}(\lambda,\ \Delta_{\text{challenge}})`$
Returned State	$`\texttt{Initialized} \left\{ \text{parametrized} \leftarrowtail (\lambda,\ I),\ \text{group} \leftarrowtail \mathbb{G},\ \text{discriminant} \leftarrowtail \Delta,\ \text{operation} \leftarrowtail \cdot , \ \text{epochId}_e \leftarrowtail \text{epochId}_e ,\ \text{pre-}\eta_e \leftarrowtail \text{pre-}\eta_e \right\}`$

3.2.3.2. Tick Commands & Grace Period

AwaitingComputationPhase	$`\Phi.\text{Stream.State} \in \texttt{AwaitingComputationPhase} : \left\{ \text{initialized} \in \texttt{Initialized},\ \text{currentSlot} \in\ \mathbb{N} \bmod \left(10 \cdot \frac{k}{f}\right) \right\}`$
Fields	$`\text{initialized} \in \texttt{Initialized}`$ — Reference to the prior initialization. $`\text{currentSlot} \in\ \mathbb{N} \bmod \left(10 \cdot \frac{k}{f}\right)`$ — The current slot in the chain timeline.

Initial tick transition to AwaitingComputationPhase:

tick	$\Phi.\text{Stream.State} \leftarrow \Phi.\text{tick}(\text{initializedState})$
Input Parameters	$\text{initializedState} \in \texttt{Initialized}$ — Configuration from the prior Initialized state.
Returned State	$`\texttt{AwaitingComputationPhase} \left\{ \text{initialized} \leftarrowtail initialiinitializedzedState,\ \text{currentSlot} \leftarrowtail 0 \right\}`$

Subsequent ticks on AwaitingComputationPhase:

tick	$`\Phi.\text{Stream.State} \leftarrow \Phi.\text{tick}(\text{awaitingComputationPhaseState})`$
Input Parameters	$`\text{awaitingComputationPhaseState} \in \texttt{AwaitingComputationPhase}`$ — Configuration from the prior Initialized state.
Returned State	$` \begin{cases} \text{When } \texttt{isWithinInitializationGracePhase} :\ \texttt{AwaitingComputationPhase}\ \{ \text{initialized} ,\ \text{currentSlot++} \} \\\\ \text{When } \texttt{isWithinComputationPhase} :\ \texttt{AwaitingAttestedOutput}\ \{ \text{initialized} ,\ \text{currentSlot++} \} \end{cases}`$

3.2.4. 🟥 Computation Phase

3.2.4.1. VDF integration

We are now entering the Computation Phase. We have waited long enough for the first slot leader within the initial interval to have the opportunity to produce a block and submit the corresponding attested output. However, because the slot distribution is privately visible, leaders within the interval cannot determine whether they are the first to produce a block.

Each leader is free to adopt their own strategy for deciding whether to initiate the proof of computation. A simple and conservative approach is to wait until $`\text{currentSlot} \geq \text{nextElectedSlot} - \left(\frac{T_\Phi}{82} + C\right)`$, where $`C`$ is a small constant. At that point, the leader may begin computing. If a block has already been produced by then, the leader can either skip the computation or abort it if already in progress. This delay increases the chances that any earlier eligible leaders have already submitted their outputs, thereby minimizing the risk of redundant proofs.

To publish the first block of interval $`i \in [1..82]`$ of epoch $`e`$, the node invokes:

$$(y_i, \pi_i) \leftarrow \Phi.\text{compute}(\text{initialized} \in \texttt{Initialized},\ i \in \texttt{Interval})$$

This function internally calls the VDF primitives: $`y_i \leftarrow \texttt{VDF.Evaluate}((\mathbb{G},\ \Delta,\ \cdot), \ x_i,\ I)`$ and $`\pi \leftarrow \texttt{VDF.Prove}((\mathbb{G},\ \Delta, \cdot),\ x_i,\ y_i,\ I)`$ with inputs constructed as:

• $`x_i \leftarrow \text{Hash}(\text{b``challenge"} ||\ \text{bin}(e) ||\ \text{pre-}\eta_e || \text{bin}(i))`$
• The parameters $`(\mathbb{G}, \Delta, \cdot)`$ and $`I`$ are retrieved from the Initialized state.

Finally, the node includes the attested outputs in the block header:

• $`y_i`$: the VDF output for interval $`i`$
• $`\pi_i`$: the corresponding VDF proof for interval $`i`$

In rare cases, an interval may produce no block, and consequently, no expected proof for the corresponding iteration. The computation phase simply acknowledges these gaps; they are handled during the subsequent Catch-up Phase, which is specifically designed to resolve such missing outputs.

3.2.4.2. The States

During the computation phase, the stream alternates between two closely related states: AwaitingAttestedOutput and AttestedOutputProvided. These two states are structurally identical, meaning they share the same underlying fields. What distinguishes them is their semantic role in the protocol’s lifecycle:

• AwaitingAttestedOutput represents the period before an attestation has been submitted for the current interval.
• AttestedOutputProvided signals that the attestation for the current interval has been successfully received and verified.

The field structure for both is as follows:

$$\Phi.\text{Stream.State} \in \texttt{AwaitingAttestedOutput} : \left\{ \begin{aligned} &\text{initialized} &&\in\ \texttt{Initialized}, \\ &\text{currentSlot} &&\in\ \mathbb{N} \bmod \left(10 \cdot \frac{k}{f}\right), \\ &\text{attestedOutputs} &&\in\ \left[\texttt{Maybe}\ (y, \pi)\right]^{82} \end{aligned} \right\}$$

Field	Description
$`\text{initialized} \in \texttt{Initialized}`$	Reference to the prior initialization state.
$`\text{currentSlot} \in\ \mathbb{N} \bmod \left(10 \cdot \frac{k}{f}\right)`$	The current slot in the timeline.
$`\text{attestedOutputs} \in \left[\texttt{Maybe}\ (y, \pi)\right]^{82}`$	An array of optional attested outputs, one per computation interval. Each index corresponds to a specific interval and may contain a proof pair $`(y, \pi)`$. If the output is not yet submitted, the entry is None.

The AttestedOutputProvided state reuses the exact same structure:

$$\Phi.\text{Stream.State} \in \texttt{AttestedOutputProvided} : \left\{ \begin{aligned} &\text{initialized} &&\in\ \texttt{Initialized}, \\ &\text{currentSlot} &&\in\ \mathbb{N} \bmod \left(10 \cdot \frac{k}{f}\right), \\ &\text{attestedOutputs} &&\in\ \left[\texttt{Maybe}\ (y, \pi)\right]^{82} \end{aligned} \right\}$$

This version aligns both the field names and their types in two neat columns. Let me know if you'd prefer the braces to be placed differently (e.g. outside the alignment block) for aesthetic reasons.

Field	Description
$`\text{initialized} \in \texttt{Initialized}`$	Reference to the prior initialization state.
$`\text{currentSlot} \in\ \mathbb{N} \bmod \left(10 \cdot \frac{k}{f}\right)`$	The current slot in the timeline.
$`\text{attestedOutputs} \in \left[\texttt{Maybe}\ (y, \pi)\right]^{82}`$	An array of optional attested outputs, one per computation interval. Each index corresponds to a specific interval and may contain a proof pair $`(y, \pi)`$. If the output hasn't been submitted yet, the entry is None. For the current interval, the output has already been provided in this state.

3.2.4.3. ProvideAttestedOutput & Tick Commands

The provideAttestedOutput command is used to submit a new attested output $`\phi_i = (y_i, \pi_i)`$ for a specific interval $`i`$, when the protocol is in the AwaitingAttestedOutput state. This function verifies the validity of the provided proof and updates the stream state accordingly :

provideAttestedOutput	$`\Phi.\text{Stream.State} \leftarrow \Phi.\text{provideAttestedOutput}(\text{awaitingAttestedOutputState},\ \phi_i)`$
Input Parameters	$`\text{awaitingAttestedOutputState} \in \texttt{AwaitingAttestedOutput}`$ — Current state awaiting an attested output $`\phi_i`$ for interval $`i`$. $`\phi_i = (y_i, \pi_i)`$ — Attested output and corresponding proof.
Property Check	Ensure $`\phi_i`$ is valid by verifying: $`\texttt{VDF.Verify}((\mathbb{G},\ \Delta,\ \cdot),\ x_i,\ y_i,\ I,\ \pi_i)`$ Where: $`x_i = \text{Hash}(\text{b``challenge"}\ \|\|\ \text{bin}(e)\ \|\|\ \text{pre-}\eta_e\ \|\|\ \text{bin}(i))`$ $`I \in \mathbb{N}`$ is the per-interval iteration count.
Returned State	$`\texttt{AttestedOutputProvided}\ \{ \text{initialized},\ \text{currentSlot} + 1,\ \text{attestedOutputs}[i] \leftarrowtail \phi_i \}`$ — Updated state reflecting the verified attestation.

Once an attested output has been provided, the next slot may trigger a tick event. If no further action is taken, the system must determine whether it remains within the current interval, moves to the next, or enters the catch-up phase. The following command captures this logic when starting from the AttestedOutputProvided state :

tick	$`\Phi.\text{Stream.State} \leftarrow \Phi.\text{tick}(\text{attestedOutputProvidedState})`$
Input Parameters	$`\text{attestedOutputProvidedState} \in \texttt{AttestedOutputProvided}`$ — The current state after an attestation has been successfully provided.
Returned State	$`\begin{cases} \text{When } \texttt{isWithinCurrentInterval} &: \texttt{AttestedOutputProvided} \{ \dots,\ \text{currentSlot++} \} \\\\ \text{When } \texttt{isWithinNextInterval} &: \texttt{AwaitingAttestedOutput} \{ \dots,\ \text{currentSlot++} \} \\\\ \text{When } \texttt{isWithinCatchUpPhase} &: \texttt{AwaitingMissingAttestedOutput} \{ \dots,\ \text{currentSlot++} \} \end{cases}`$

Alternatively, when still waiting for an attestation and no block was produced, a tick may trigger a transition based on the current time. This command applies to the AwaitingAttestedOutput state before any attestation has been submitted :

tick	$`\Phi.\text{Stream.State} \leftarrow \Phi.\text{tick}(\text{awaitingAttestedOutputState})`$
Input Parameters	$`\text{awaitingAttestedOutputState} \in \texttt{AwaitingAttestedOutput}`$ — Current state awaiting an attested output $`\phi_i`$ for interval $`i`$. $`\phi_i = (y_i, \pi_i)`$ — Attested output and corresponding proof.
Returned State	$` \begin{cases} \text{When } \texttt{isWithinCurrentInterval} :\ \texttt{AwaitingComputationPhase}\ \{ \text{..} ,\ \text{currentSlot++} \} \\\\ \text{When } \texttt{isWithinCatchUpPhase} :\ \texttt{AwaitingMissingAttestedOutput}\ \{ \text{..} ,\ \text{currentSlot++} \} \\\\ \text{When } \texttt{isClosable} :\ \texttt{AwaitingGracefulClosure}\ \{ \text{..} ,\ \text{currentSlot++} \}\end{cases}`$

isClosable indicates that all attested outputs have been successfully provided, and only the final interval remains, during which the outputs are aggregated and the seed $`\eta_e`$ is derived and recorded on-chain.

3.2.5. 🟦 Catch-up Phase

This Catch-up Phase closely resembles the preceding Computation Phase, but its purpose is to recover from any blockless intervals that may have occurred — albeit such cases are extremely rare.

The phase spans a total of 37 intervals: 36 are reserved to account for up to 36 consecutive intervals without block production (e.g., a global outage affecting 30% of an epoch), and 1 final interval is allocated for the Closure Phase. As in the Computation Phase, missing attested outputs must be submitted in order, one per interval.

The faster these missing outputs are provided, the sooner the state machine can transition to the final phase. Although the protocol allocates 37 intervals to handle the worst-case scenario, recovery may complete much earlier in practice.

This section focuses solely on the Catch-up Phase; the next section will describe the process of stream closure.

3.2.5.1. The States

Structurally, we define two states that are similar in form and semantics to AwaitingMissingAttestedOutput and AttestedMissingOutputProvided:

$$\Phi.\text{Stream.State} \in \texttt{AwaitingMissingAttestedOutput} : \left\{ \begin{aligned} &\text{initialized} &&\in\ \texttt{Initialized}, \\ &\text{currentSlot} &&\in\ \mathbb{N} \bmod \left(10 \cdot \frac{k}{f}\right), \\ &\text{attestedOutputs} &&\in\ \left[\texttt{Maybe}\ (y, \pi)\right]^{82} \end{aligned} \right\}$$ $$\Phi.\text{Stream.State} \in \texttt{AttestedMissingOutputProvided} : \left\{ \begin{aligned} &\text{initialized} &&\in\ \texttt{Initialized}, \\ &\text{currentSlot} &&\in\ \mathbb{N} \bmod \left(10 \cdot \frac{k}{f}\right), \\ &\text{attestedOutputs} &&\in\ \left[\texttt{Maybe}\ (y, \pi)\right]^{82} \end{aligned} \right\}$$

This phase focuses on recovering the missing attested outputs—specifically, the None entries in the attestedOutputs array. The goal during this phase is to have those missing values provided.This phase operates under strict sequential expectations where the missing attested outputs must be provided in order, one per interval, as in the Computation Phase. To make this explicit, we define the sequence of expected indices as follows:

$$\text{ExpectedMissingIndices} := \left\{ i \in \{1, \dots, 82\} \mid \text{attestedOutputs}[i] = \texttt{Nothing} \right\}$$

This ordered set defines the exact sequence in which the missing attestations must be submitted during the Catch-up Phase.

3.2.5.2. ProvideMissingAttestedOutput & Tick Commands

The provideMissingAttestedOutput command is used to submit a missing attested output $`\phi_i = (y_i, \pi_i)`$ for a specific interval $`i`$, when the protocol is in the AwaitingMissingAttestedOutput state. This function checks the validity of the proof and updates the stream state accordingly:

provideMissingAttestedOutput	$`\Phi.\text{Stream.State} \leftarrow \Phi.\text{provideMissingAttestedOutput}(\text{awaitingMissingAttestedOutputState},\ \phi_i)`$
Input Parameters	$`\text{awaitingMissingAttestedOutputState} \in \texttt{AwaitingMissingAttestedOutput}`$ — State awaiting a missing attestation $`\phi_i`$ for interval $`i`$. $`\phi_i = (y_i, \pi_i)`$ — Attested output and its proof.
Property Check	Verify $`\phi_i`$ with: $`\texttt{VDF.Verify}((\mathbb{G},\ \Delta,\ \cdot),\ x_i,\ y_i,\ I,\ \pi_i)`$ Where: $`x_i = \text{Hash}(\text{b``challenge"}\ \|\|\ \text{bin}(e)\ \|\|\ \text{pre-}\eta_e\ \|\|\ \text{bin}(i))`$ $`I \in \mathbb{N}`$ is the per-interval iteration count.
Returned State	$`\texttt{MissingAttestedOutputProvided} \{ \text{initialized},\ \text{currentSlot} + 1,\ \text{attestedOutputs}[i] \leftarrowtail \phi_i \}`$ — Updated state reflecting the accepted missing output.

Once a missing attested output has been provided, the next slot may trigger a tick event. The system must determine whether it remains within the current interval, moves to the next, or enters the closure phase. The following command captures this logic when starting from the MissingAttestedOutputProvided state :

tick	$`\Phi.\text{Stream.State} \leftarrow \Phi.\text{tick}(\text{missingAttestedOutputProvidedState})`$
Input Parameters	$`\text{missingAttestedOutputProvidedState} \in \texttt{MissingAttestedOutputProvided}`$ — The current state after an attestation has been successfully provided.
Returned State	$`\begin{cases} \text{When } \texttt{isWithinCurrentInterval} &: \texttt{MissingAttestedOutputProvided} \{ \dots,\ \text{currentSlot++} \} \\\\ \text{When } \texttt{isWithinNextInterval} &: \texttt{AwaitingMissingAttestedOutput} \{ \dots,\ \text{currentSlot++} \} \\\\ \text{When } \texttt{isClosable} &: \texttt{AwaitingGracefulClosure} \{ \dots,\ \text{currentSlot++} \} \\\\ \text{When } \texttt{isUngracefullyClosable} &: \texttt{UngracefullyClosed} \{.., {pre-}\eta_e = {initialized.}{pre-}\eta_e \} \} \end{cases}`$

Alternatively, when still waiting for an attestation and no block was produced, a tick may trigger a transition based on the current time. This command applies to the AwaitingMissingAttestedOutput state before any attestation has been submitted :

tick	$`\Phi.\text{Stream.State} \leftarrow \Phi.\text{tick}(\text{awaitingMissingAttestedOutputState})`$
Input Parameters	$`\text{awaitingMissingAttestedOutputState} \in \texttt{AwaitingMissingAttestedOutput}`$ — Current state awaiting an attested output $`\phi_i`$ for interval $`i`$. $`\phi_i = (y_i, \pi_i)`$ — Attested output and corresponding proof.
Returned State	$` \begin{cases} \text{When } \texttt{isWithinCurrentInterval} :\ \texttt{AwaitingMissingAttestedOutput}\ \{ \text{..} ,\ \text{currentSlot++} \} \\\\ \text{When } \texttt{isClosable} :\ \texttt{AwaitingGracefulClosure}\ \{ \text{..} ,\ \text{currentSlot++} \} \\\\ \text{When } \texttt{isUngracefullyClosable} :\ \texttt{UngracefullyClosed} \{.., {pre-}\eta_e = {initialized.}{pre-}\eta_e \} \}\end{cases}`$

isUngracefullyClosable indicates that the end of the lifecycle segment has been reached (i.e., currentSlot++ == 0), while some attested outputs are still missing. When this condition holds, the lifecycle is forcefully closed in an ungraceful manner.

3.2.6 ⬛ Closure Phase

We now enter the final phase of the lifecycle, during which all collected outputs are expected to be aggregated and recorded on-chain, and the seed $\eta_e$ derived and committed.

Successful Scenarios: In these cases, all attested outputs have been provided by the end of the catch-up phase.

• Best-case scenario: The closure phase begins at interval 84, giving the system 37 intervals to perform output aggregation and seed commitment under normal operating conditions.
• Worst-case scenario: The catch-up mechanism is fully utilized, and the system enters the closure phase at interval 120, the very last interval of the lifecycle segment. Even so, all necessary outputs have been successfully provided.

Failure Scenario:

This occurs when the lifecycle segment reaches its end (i.e., the full $10 \cdot \frac{k}{f}$ slots), and despite the entire duration of the catch-up mechanism (up to interval 120), either some required attested outputs remain missing, or all outputs have been delivered but the final aggregation has not occurred. This scenario represents an extremely rare event—statistically far beyond 128-bit confidence—and reflects a severe disruption in which no blocks have been produced for over 36 hours. These edge cases are represented in the diagram by the transition Tick / isUngracefullyClosable.

3.2.6.1. The States

In this phase, we define two states:

• AwaitingGracefulClosure: This state signifies that all 82 attested outputs have been successfully collected. At this point, the outputs are no longer optional—each index is populated with a verified pair $`(y, \pi)`$.

$$\Phi.\text{Stream.State} \in \texttt{AwaitingGracefulClosure} : \left\{ \begin{aligned} &\text{initialized} &&\in\ \texttt{Initialized}, \\ &\text{currentSlot} &&\in\ \mathbb{N} \bmod \left(10 \cdot \frac{k}{f}\right), \\ &\text{attestedOutputs} &&\in\ \left[(y, \pi)\right]^{82} \end{aligned} \right\}$$

• Closed: This is a final state in the stream lifecycle. It signifies that the aggregated output has been computed and verified, and the final epoch randomness $\eta_e$ has been successfully derived—achieving the core objective of the protocol. This state is reached in response to either a Close command :

$$\Phi.\text{Stream.State} \in \texttt{Closed} : \left\{ \begin{aligned} &\text{initialized} &&\in\ \texttt{Initialized}, \\ &\text{attestedOutputs} &&\in\ \left[(y, \pi)\right]^{82}, \\ &\text{aggregatedOutput} &&\in\ (x, y, \pi), \\ &\eta_e &&\in\ \{0,1\}^{256} \end{aligned} \right\}$$

• UngracefullyClosed: This is a terminal state in the stream lifecycle. It indicates that either not all expected attested outputs were provided, or the aggregated output could not be computed. As a result, $`{pre-}\eta_e`$ is returned as the final value of $`\eta_e`$. Statistically, this state is highly unlikely to occur, but it is explicitly handled for completeness and structural consistency of the state machine. The transition to this state is triggered by Tick in combination with the isUngracefullyClosable condition.

$$\Phi.\text{Stream.State} \in \texttt{UngracefullyClosed} : \left\{ \begin{aligned} &\text{initialized} &&\in\ \texttt{Initialized}, \\ &\text{attestedOutputs} &&\in\ \left[\texttt{Maybe}\ (y, \pi)\right]^{82} \\ &{pre-}\eta_e &&\in\ \{0,1\}^{256} \end{aligned} \right\}$$

3.2.6.2. The Successful Scenario: The Close Command

At this stage, the system is in the AwaitingGracefulClosure state. All necessary data has been collected, and a block can now be produced within the remaining time before the end of the stream lifecycle (as previously discussed, this could occur at the 84th or 120th interval, depending on how smoothly the lifecycle progressed).

In this scenario, the first block producer within the remaining intervals must include the following values in the block body:

• $`(y, \pi)`$: The aggregated output of the $`\Phi`$ computation, representing the final result and its corresponding proof.
• $`\eta_e`$: The final objective of the protocol—a 256-bit epoch randomness beacon, which will be used to seed leader election in the next epoch.

These values complete the stream and trigger the transition to the Closed state.

Close	$`\Phi.\text{Stream.State} \leftarrow \Phi.\text{Close}((x, y, \pi),\ \text{awaitingGracefulClosureState})`$
Input Parameters	$`\text{awaitingGracefulClosureState} \in \texttt{AwaitingGracefulClosure}`$ — State indicating readiness for closure. $`(y,\ \pi)`$ — Aggregated output and its proof for the entire stream.
Property Check	Verify the aggregated output with: $`\texttt{VDF.Aggregation.Verify}((\mathbb{G},\ \Delta,\ \cdot),\ \lambda,\ x,\ y,\ \text{attestedOutputs},\ \pi)`$ Where: $`\lambda`$ is the security parameter, $`x`$ is the aggregated input of the $`\Phi`$ computation $`\text{attestedOutputs} = \text{awaitingGracefulClosureState.attestedOutputs}`$
Epoch Randomness	$`\eta_e = \text{Hash}^{(256)}(y)`$ — Apply the SHA-256 hash function to $`y`$.
Returned State	$`\texttt{Closed} \{ \text{initialized},\ \text{attestedOutputs},\ (x, y, \pi),\ \eta_e \}`$ — Final state embedding the verified computation and the derived epoch randomness.

3.2.6.3. tick Command

The tick command handles time progression within the AwaitingGracefulClosure state:

• isUngracefullyClosable is true when the stream reaches the end of its lifecycle segment (i.e., $`\texttt{currentSlot} + 1 \equiv 0 \pmod{T}`$) and some attested outputs are still missing. When this condition holds, the system transitions to the UngracefullyClosed state.

• Otherwise, the command simply increments the currentSlot field to reflect time advancement.

tick	$`\Phi.\text{Stream.State} \leftarrow \Phi.\text{tick}(\text{awaitingGracefulClosureState})`$
Input Parameters	$`\text{awaitingGracefulClosureState} \in \texttt{AwaitingMissingAttestedOutput}`$ — State indicating readiness for closure.
Returned State	$`\begin{cases} \text{When } \texttt{isUngracefullyClosable} :\ \texttt{UngracefullyClosed} \{.., {pre-}\eta_e = {initialized.}{pre-}\eta_e \} \\\\ \text{Otherwise} :\ \texttt{AwaitingGracefulClosure} \{\, \ldots,\, \texttt{currentSlot} + 1 \,\} \end{cases}`$

isUngracefullyClosable indicates that the end of the lifecycle segment has been reached (i.e., currentSlot++ == 0), while some attested outputs are still missing. When this condition holds, the lifecycle is forcefully closed in an ungraceful manner. Otherwise we are just update the current slot field

3.2.6.4. The Failure Scenario: Ungraceful Closure

If the protocol reaches the end of its lifecycle, or it becomes evident that too many consecutive blockless intervals have occurred—such that a valid $`\eta_e`$ can no longer be derived—the Tick signal triggers the isUngracefullyClosable condition. This causes a transition to the terminal state UngracefullyClosed, in which the precomputed value $`{pre-}\eta_e`$ is adopted as the official $`\eta_e`$.

While this state is statistically unexpected, it is explicitly defined to ensure completeness and structural consistency within the state machine.

4. Recommended Parameter values

There are two categories of parameters in the Phalanx protocol that Cardano governance will need to oversee. The first category concerns the VDF parameters, which are essential to maintaining the protocol’s cryptographic security. The second concerns the total time budget $T_\Phi$ that will be required from SPOs during the Computation Phase.

The goal of this section is to provide recommended values for these parameters along with the rationale behind their selection, so that governance is well-equipped to adjust them over time in response to advances in adversarial computational power.

4.1 VDF Security Parameters λ and ρ

The VDF component in Phalanx relies on class group security, which is parameterized by two values:

• $`\lambda`$, the class group security parameter, and
• $`\rho`$, the grinding resistance parameter, newly introduced in the Phalanx design.

Several combinations of $`\lambda`$ and $`\rho`$ are considered in the literature, depending on the desired level of paranoia or efficiency. Based on the recommendations from the paper Trustless Unknown-Order Groups, we highlight the following trade-offs:

• A paranoid setting, $(\lambda, \rho) = (128, 128)$, requires a group size of ~3400 bits.

• A more realistic yet cautious setting, $(\lambda, \rho) = (128, 55)$, brings the group size down to ~1900 bits, but requires discriminants of at least 3800 bits.

• Based on those benchmarks and our needs, we opt for $(\lambda, \rho) = (128, 64)$, which corresponds to:

  • a discriminant size of 4096 bits,
  • and a group size of 2048 bits.

This strikes a balance between long-term security and practical efficiency:

• On one hand, breaking the class group is considered harder than finding a collision in a 256-bit hash (our minimum security baseline).
• On the other hand, by following the paper’s recommendation and selecting a slightly lower $`\rho = 64`$, we can reduce the size of on-chain group elements while maintaining sufficient resistance against grinding.

Since Phalanx is designed to operate with a single class group instance “for the lifetime of the protocol” (reparametrization would require explicit governance intervention), this configuration $(\lambda, \rho) = (128, 64)$ ensures protocol simplicity, consistency, and operational predictability.

4.2 Time Budget Tᵩ and Derived T

In terms of efficiency, the section 1. How Phalanx Addresses CPS-21 – Ouroboros Randomness Manipulation in the Rationale part of this document illustrates, through three scenarios $`\text{Phalanx}_{1/10}`$, $`\text{Phalanx}_{1/100}`$, and $`\text{Phalanx}_{\text{max}}`$, how different time budgets (2 hours, 12 hours, and 5 days, respectively) improve the protocol’s security guarantees against grinding attacks.

In terms of computational load, we recommend setting the time budget at a midpoint between minimal and maximal protocol capacity, corresponding to approximately 12 hours of execution on typical, CPU-based hardware as recommended for SPOs. However, this choice should ultimately be guided by settlement time performance requirements across the ecosystem, including the needs of partner chains and other dependent components.

4.2.1 Specialized ASIC vs CPU-Based Chips

We need to account for the possibility that adversaries may equip themselves with specialized ASIC chips optimized for computing Wesolowski’s Verifiable Delay Function (VDF). The Chia team has already developed and deployed such ASIC Timelords, which demonstrate between 3× and 5× performance improvements compared to standard CPU-based implementations. These ASICs reach up to 1,000,000 iterations per second, while commodity CPU Timelords typically max out around 260,000 IPS (Chia Network, Oct 2023).

To mitigate this performance asymmetry, our initial strategy is to require a 12-hour equivalent workload on standard CPU hardware (as in $`\text{Phalanx}_{1/10}`$), which is calibrated to provide the same security guarantees as a less aggressive configuration like $`\text{Phalanx}_{1/100}`$. This gives us a conservative baseline for security, assuming an adversary might leverage ASIC acceleration.

Critically, scaling this kind of grinding capability is expensive. For an adversary to mount an effective grinding attack, they would need to build and operate a farm of VDF-optimized ASICs — a non-trivial financial and operational challenge. Chia’s rollout of these units has been tightly controlled and aimed at ensuring global distribution, not centralization (Chia Global Expansion Update, June 2024).

Mid-term, we propose encouraging — or potentially requiring — stake pool operators (SPOs) to adopt VDF ASIC hardware. This would ensure that honest participants remain competitive and are not systematically outperformed by well-resourced adversaries.

Long-term, our strategy involves standardizing the use of verifiable delay ASICs across the network, or alternatively, establishing a dynamic calibration process. This would allow iteration requirements to be periodically adjusted based on the evolving performance gap between commodity and specialized hardware, maintaining consistent and predictable security guarantees.

In summary, while ASIC-equipped adversaries could, in theory, gain a computational advantage during the grinding window, the cost and scale required to pose a real threat remains high. Our mitigation strategy is to raise the honest baseline to neutralize this advantage and prepare for possible hardware evolution over time.

4.2.1 Deriving from Tᵩ to T

We recommend a 12-hour computation budget on standard CPU-based machines, which we estimate to be 10× slower than specialized ASICs available to adversaries. This configuration corresponds to Phalanx_1/10 in terms of time budget, while achieving Phalanx_1/100 in terms of security guarantees against grinding attacks.

However, this time budget ($T\_\Phi$) is a high-level abstraction. To implement it concretely, we must derive the number of VDF iterations ($T$) required for each first block of an interval. Assuming 82 intervals per epoch, this translates to:

$$T = \frac{T_\Phi}{82} = \frac{12 \text{ hours} \times 3600 \text{ seconds/hour}}{82} \approx 527 \text{ seconds}$$

So, we ask for approximately 10 minutes of VDF computation per published interval block on standard CPU-based hardware.

To translate this into a concrete number of VDF iterations ($T$), we rely on performance benchmarks from the implementation available in the repository rrtoledo/chiavdf. This library is a highly optimized and production-hardened implementation of Wesolowski's VDF, currently in use by the Chia blockchain. We have made minor, superficial modifications to this codebase solely to facilitate benchmarking and increase the discriminant size.

Thanks to its well-established performance profile, this implementation provides a dependable baseline for estimating how many iterations can be executed within a fixed time frame on standard CPU hardware. Under our test environment—an Ubuntu machine equipped with an Intel® Core™ i9-14900HX (32 cores, 64 GiB RAM)—we observed approximately 27 million iterations in a 10-minute window.

Note : We recommend that this benchmark be re-run on a dedicated, representative SPO machine to calibrate a more accurate production value for $T$.

5. Efficiency analysis

5.1 Block Publication

To publish a block, a node must:

• Perform $T$ squarings to compute the output,
• Execute $O(T / \log(T))$ operations for the proof generation.

We now show benchmarks for evaluating and proving together VDFs, as well as individually, for different discriminant sizes done on a Ubuntu computer with Intel® Core™ i9-14900HX with 32 cores and 64.0 GiB RAM. For a 4,096 bit long discriminant, we perform around 45,000 iterations per second, and so evaluate and prove a VDF in 22.6s.

Size Discriminant	#iterations	IPS	Evaluate and Prove (s)	σ proving	Eval (s)	σ proving	Prove (s)	σ proving
256	10,000	637252	0.0187	0.000676	1.57E-02 (84%)	0.000563	8.00E-03 (43%)	0.000461
256	100,000	641349	0.172	0.00115	1.56E-01 (91%)	0.00188	5.68E-02 (33%)	0.00165
256	1,000,000	627336	1.72	0.0215	1.59E+00 (93%)	0.0197	4.88E-01 (29%)	0.00633
512	10,000	367449	0.0322	0.000635	2.72E-02 (85%)	0.000648	1.31E-02 (41%)	0.000204
512	100,000	378942	0.289	0.0029	2.64E-01 (92%)	0.00283	8.76E-02 (31%)	0.000893
512	1,000,000	378204	2.83	0.0287	2.64E+00 (94%)	0.0279	7.29E-01 (26%)	0.00873
1024	10,000	206186	0.0537	0.000902	4.85E-02 (91%)	0.00076	2.00E-02 (38%)	0.000364
1024	100,000	211921	0.503	0.00722	4.72E-01 (94%)	0.00721	1.45E-01 (29%)	0.00198
1024	1,000,000	213319	4.92	0.0506	4.69E+00 (96%)	0.0475	1.20E+00 (25%)	0.0136
2048	10,000	103135	0.105	0.000285	9.70E-02 (92%)	0.000303	3.77E-02 (36%)	0.000122
2048	100,000	105315	1.01	0.0165	9.50E-01 (94%)	0.0123	2.78E-01 (28%)	0.00516
2048	1,000,000	107038	9.75	0.0746	9.34E+00 (96%)	0.0828	2.20E+00 (23%)	0.0209
4096	10,000	44567.8	0.244	0.00463	2.24E-01 (92%)	0.00454	8.30E-02 (35%)	0.00168
4096	100,000	45848.6	2.31	0.0253	2.18E+00 (95%)	0.0229	6.00E-01 (26%)	0.0089
4096	1,000,000	46293.2	22.6	0.16	2.16E+01 (96%)	0.148	4.79E+00 (22%)	0.0422

5.2 Block Verification

5.2.1 When Not Syncing

To verify a VDF proof, a node performs:

• 2 hashes,
• 4 small exponentiations,
• 3 group multiplications.

Over an epoch with $N$ intervals, this results in:

• $2 \cdot N$ hashes,
• $4 \cdot N$ small exponentiations,
• $3 \cdot N$ group multiplications.

We now show verification benchmarks for discriminants of different sizes done on the same machine as before. For a 4,096 bit long discriminant, the verification takes around 15ms.

Size Discriminant	#iterations	Verification (ms)	σ verification
256	10,000	1.74E+00 (10%)	0.0786
256	100,000	1.12E+00 (1%)	0.0471
256	1,000,000	1.75E+00 (1%)	0.151
512	10,000	3.25E+00 (11%)	0.0562
512	100,000	1.89E+00 (1%)	0.0268
512	1,000,000	2.11E+00 (1%)	0.134
1024	10,000	3.66E+00 (7%)	0.117
1024	100,000	3.21E+00 (1%)	0.0467
1024	1,000,000	3.20E+00 (1%)	0.135
2048	10,000	7.00E+00 (7%)	0.0409
2048	100,000	9.33E+00 (1%)	0.147
2048	1,000,000	6.40E+00 (1%)	0.218
4096	10,000	1.58E+01 (7%)	0.316
4096	100,000	1.47E+01 (1%)	0.248
4096	1,000,000	1.37E+01 (1%)	0.303

5.2.2 When Syncing

When synching, the nodes only need to update the accumulators and verify the final aggregation proof. As such, the node perform in total arounf half as less operations than verifying all proofs individually. More particularly, we have:

• $2 \cdot N$ hashes,
• $2 \cdot (N + 1)$ small exponentiations.
• $2 \cdot N + 1$ group multiplications,

Note: The exponentiations involving the $\alpha_i$ values are half as expensive as those in the full proof verification.

For a discriminant of 4096 bits, we benchmarks the aggregation functions on the same machine as before. We can see that updating the accumulators in the aggregation indeed takes half time as much as verifying a single VDF proof, and verifying the aggregation is as cheap as a normal VDF proof and that proving the aggregation is more expensive than a VDF output, this is due to the absence of intermediary value found when evaluating the VDF input, but less expensive than evaluating a VDF.

Size Discriminant	#iterations	$`\texttt{VDF.Aggregation.Update}`$ (ms)	$`\texttt{VDF.Aggregation.Prove}`$ (s)	$`\texttt{VDF.Aggregation.Verify}`$ (ms)
$4096$	1,000	8.0E+00	2.3E-03	1.7E+01
$4096$	10,000	8.0E+00	3.0E-02	1.7E+01
$4096$	100,000	8.0E+00	3.0E+00	1.7E+01
$4096$	1,000,000	8.0E+00	3.1E+01	1.7E+01

6. CDDL Schema for the Ledger

To support Phalanx, one block per interval (every 3600 slots), across 83 intervals per epoch, must include 2 group elements. Each of these elements can be compressed to approximately $3/4 \cdot \log_2(|\Delta|)$ bits. Based on our recommended discriminant size of 4096 bits:

• 3,104 bits (388 bytes) per element (the benchmarked library adds 4 bytes to each element),
• 6,208 bits (776 bytes) per block (2 elements),
• 515,264 bits (64,408 bytes ≈ 64.4 KB) per epoch (83 blocks).

Phalanx requires a single addition to the block body structure in the ledger: the field phalanx_challenge.

 block =
   [ header
   , transaction_bodies         : [* transaction_body]
   , transaction_witness_sets   : [* transaction_witness_set]
   , auxiliary_data_set         : {* transaction_index => auxiliary_data }
   , invalid_transactions       : [* transaction_index ]
+  , ? phalanx_challenge        : vdf_attested_output
   ]

The structure phalanx_challenge is defined as follows:

vdf_attested_output =
  [ output : vdf_size
  , proof  : vdf_size
  ]
 
vdf_size = [ bytes, bytes .size 388 ]

We initially evaluated including the phalanx_challenge (i.e., the VDF attested output) in the block header (instead as proposed in the block body) colocated with the VRF outputs. However, this approach raised concerns due to header size constraints.

The current maximum block header size in Cardano is 1100 bytes, although actual usage today averages around 860 bytes. Since TCP packet limits suggest keeping headers under 1500 bytes (1,460 without headers), the available headroom is approximately 600 bytes. The full vdf_attested_output in its default form requires:

• 388 bytes per group element (assuming the lowest acceptable security parameters)
• 2 group elements (output + proof)
• Total: 776 bytes

This would exceed the 1500-bytes limit, risking fragmentation and violating guidance from the Cardano networking team. We could safely decrease the group element size by decreasing the security parameters if we were to generate new class groups at each epoch. Doing so would however render the protocol more complex and potentially weaken the security of the protocol as we may have more chances to generate a weak class group.

Rationale: How does this CIP achieve its goals?

1. How Phalanx Addresses CPS-21 - Ouroboros Randomness Manipulation?

1.1 Problem Overview

CPS-0021 / Ouroboros Randomness Manipulation examines the Randomness Generation Sub-Protocol within Ouroboros Praos ⚙️, highlighting its vulnerabilities and their implications for Cardano’s security 🔒. Key insights include:

• Randomness Vulnerability: Ouroboros Praos employs VRFs for randomness generation, but this approach is susceptible to grinding attacks, where adversaries manipulate outcomes to influence leader election, threatening Cardano’s fairness ⚖️ and integrity.
• Attack Likelihood: Attacks become significantly more feasible when an adversary controls over 20% of the total stake (approximately 4.36 billion ADA, as of March 2025), while smaller stakes (e.g., 5%) make such attempts highly unlikely over extended periods.
• Economic Barrier: Gaining enough stake to execute an attack requires a substantial investment 💰—billions of USD for a 20% share—posing a financial risk, as a successful attack could devalue the asset and undermine network trust.
• Computational Feasibility: The feasibility of attacks varies widely based on the computational resources an adversary can deploy, becoming progressively more accessible as stake accumulates:
  • Small-scale attacks, costing as little as ~$56, are easily achievable with minimal resources, such as a standard computer, making them a low-barrier threat that even individual actors could attempt.
  • Large-scale attacks, costing up to ~$3.1 billion, require extensive computational infrastructure, such as large data centers with millions of CPUs or ASICs, placing them in a range from feasible for well-funded entities (e.g., corporations or nation-states) to nearly impractical for most adversaries due to the immense resource demands.
  • The intensity of these attacks scales with stake: the more stake an adversary holds, the greater their influence over leader election, amplifying their ability to manipulate randomness. In a simplistic view, this can be likened to manipulating a $256$-bits nonce—a value $\rho$ ranging from $0$ to $256$— where higher stake progressively grants more control, potentially allowing full manipulation of the nonce at the upper limit.
  • The wide cost disparity reflects how the complexity of the attack—such as the scope of the targeted time window and the depth of evaluation—drastically increases resource needs, acting as a natural deterrent for more ambitious manipulations.

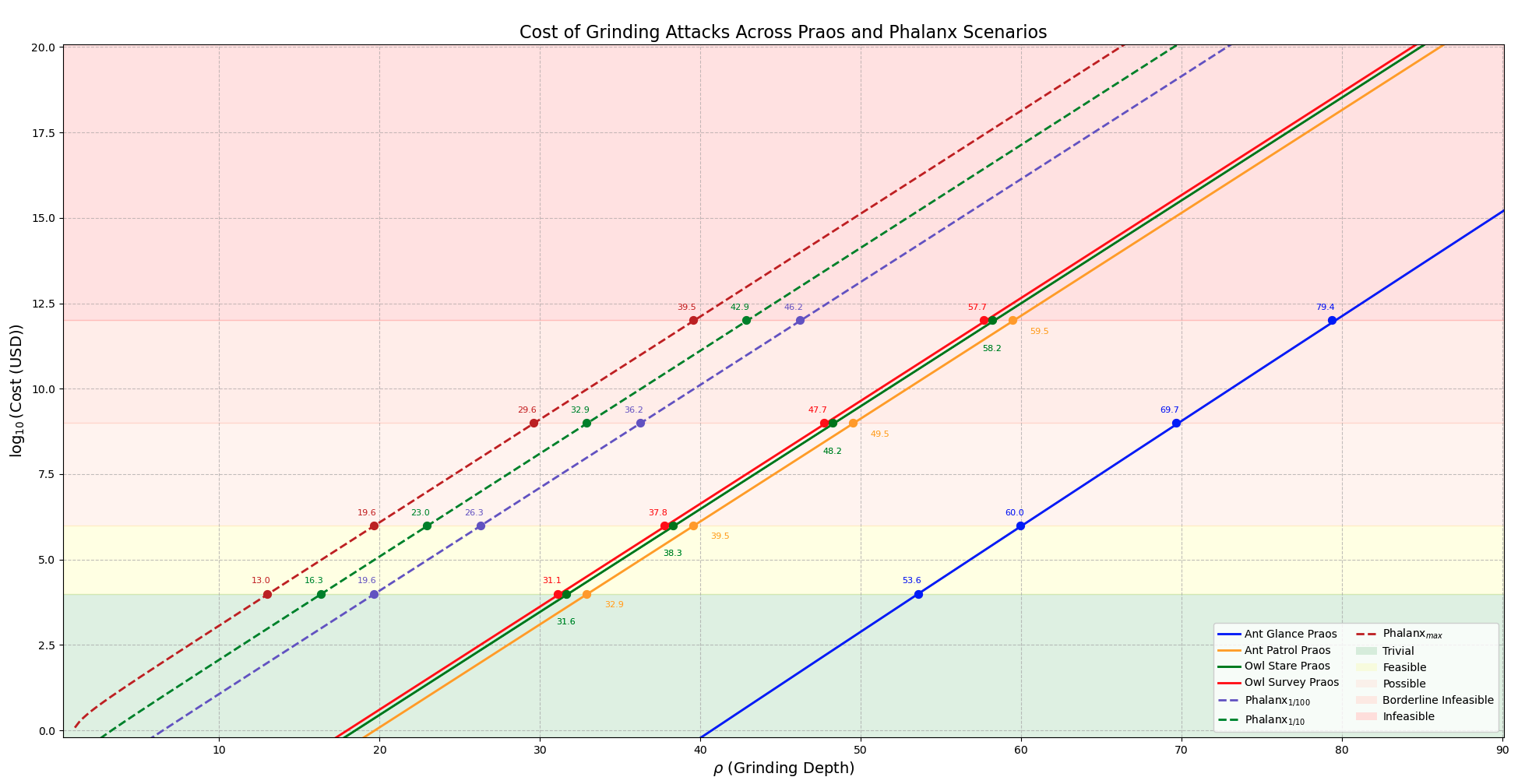
To illustrate the Computational Feasibility, the graph below (sourced from the CPD, Section 3. The Cost of Grinding: Adversarial Effort and Feasibility) maps attack feasibility across four scenarios—Ant Glance, Ant Patrol, Owl Stare, and Owl Survey—based on the nonce value $\rho$ (0 to 256 bits). Each scenario reflects different attack complexities, with feasibility shifting as computational and economic demands grow:

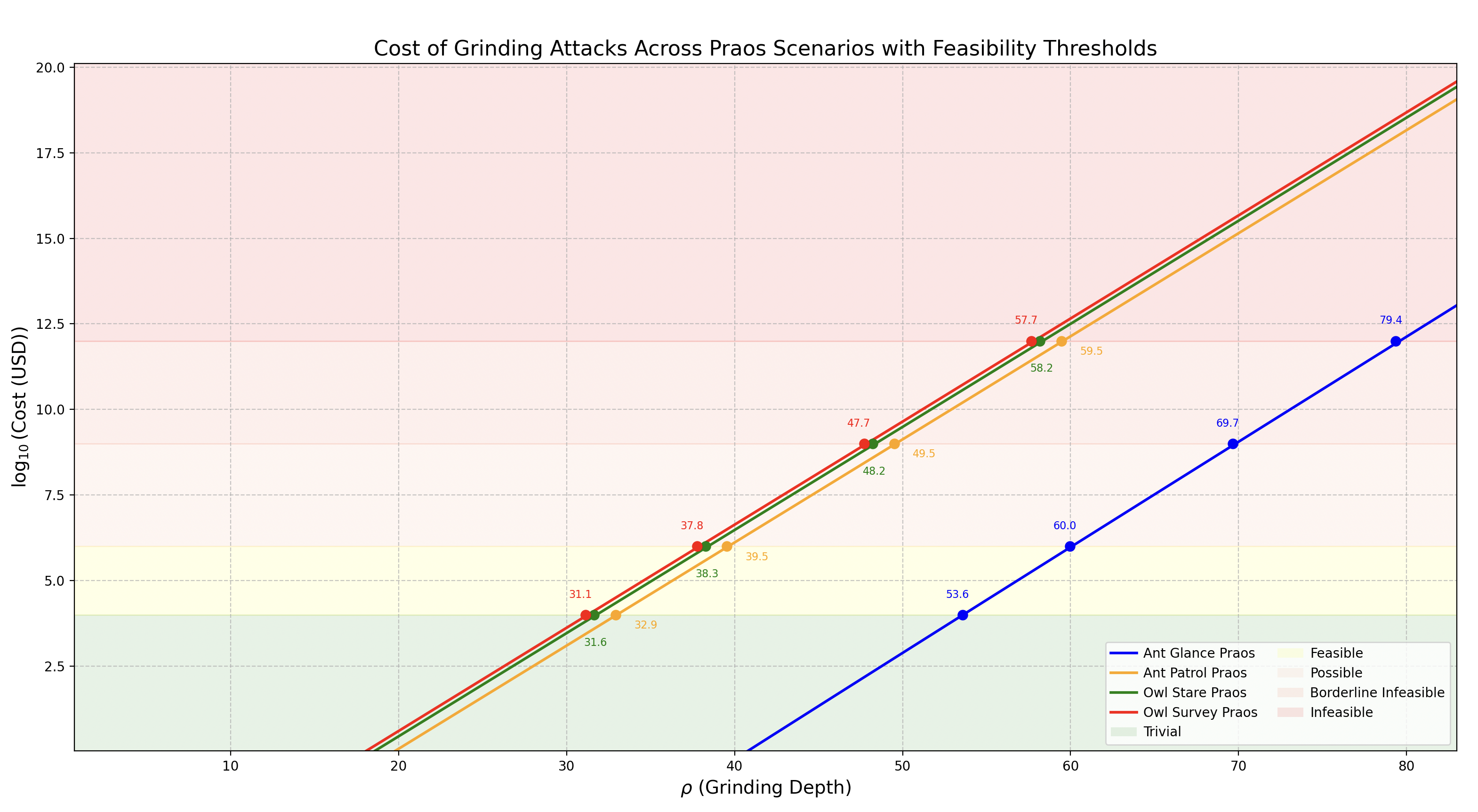
The table below delineates the $\rho$ values at which each scenario transitions across feasibility categories, illustrating the computational and economic thresholds:

Feasibility Category	🔵 Ant Glance	🟠 Ant Patrol	🟢 Owl Stare	🔴 Owl Survey
🟢 🌱 Trivial for Any Adversary	$0 \to 53.6$	$0 \to 32.9$	$0 \to 31.6$	$0 \to 31.1$
🟡 💰 Feasible with Standard Resources	$53.6 \to 60$	$32.9 \to 39.5$	$31.6 \to 38.3$	$31.1 \to 37.8$
🟠 🏭 Large-Scale Infrastructure Required	$60 \to 69.7$	$39.5 \to 49.5$	$38.2 \to 48.2$	$37.8 \to 47.7$
🔴 🚫 Borderline Infeasible	$69.7 \to 79.4$	$49.5 \to 59.5$	$48.2 \to 58.2$	$47.7 \to 57.7$
🔴 🚫 Infeasible	$79.4 \to 256$	$59.5 \to 256$	$58.2 \to 256$	$57.7 \to 256$

Context: The scenarios represent increasing attack sophistication (e.g., Ant Glance is a quick, low-effort attack; Owl Survey is a comprehensive, resource-intensive one). As $\rho$ increases, so does the difficulty, shifting feasibility from trivial (e.g., a lone actor with a laptop) to infeasible (e.g., requiring nation-state-level resources).

These thresholds reveal critical vulnerabilities in Cardano’s current consensus design. Phalanx aims to mitigate these risks. In the following section, we revisit the core computational model, introduce the proposed enhancements, and quantify how they shift the feasibility landscape in favor of security.

1.2 Phalanx Cost Amplification per Grinding Attempt

In Phalanx, we introduce an additional parameter and computational cost, denoted $T_\Phi$, for each grinding attempt. This cost represents the total cumulative effort required to compute $i$ iterations of the $\Phi$ primitive. This additional cost directly impacts the total estimated time per grinding attempt, as originally defined in CPD Section 3.3.4 - Total Estimated Time per Grinding Attempt. The baseline grinding time in Praos is:

$$T_{\text{grinding}}^{\text{Praos}} = \frac{\rho}{2} T_{\text{BLAKE2b}} + w_T \cdot ( T_{\mathsf{VRF}} + T_{\text{eligibility}} ) + T_{\text{eval}}$$

With Phalanx, the total grinding time per attempt is updated to include $T_\Phi$:

$$T_{\text{grinding}}^{\text{Phalanx}} = \frac{\rho}{2} T_{\text{BLAKE2b}} + w_T \cdot ( T_{\mathsf{VRF}} + T_{\text{eligibility}} ) + T_{\text{eval}} + T_\Phi$$

Where:

• $T_{\mathsf{VRF}}$ is the VRF evaluation time,
• $T_{\text{eligibility}}$ is the eligibility check time,
• $T_{\text{BLAKE2b}}$ is the time for the hashing operation,
• $w_T$ is the target window size (seconds),
• $\rho$ is the grinding depth,
• $T_{\text{eval}}$ is the nonce selection and evaluation time (attack-specific).
• $T_\Phi$ is the additional computational cost of Phalanx

The introduction of $T_\Phi$ substantially increases the computational burden for adversaries, as they must recompute the $\Phi^i$ function for each of the $2^\rho$ possible nonces evaluated during a grinding attack. In contrast, for honest participants, this computation is distributed across the epoch, ensuring it remains manageable and efficient.

1.3 Phalanx Cost Amplification per Grinding Attack

Building on the updated grinding time formula introduced in the previous section, which incorporates the additional computational cost $T_\Phi$, we can now revise the formula for a grinding attack from CPD Section 3.4.1 - Formula, where we defined a total attack time that must fit within the grinding opportunity window $w_O$:

$$\frac{2^{\rho} \cdot T_{\text{grinding}}^{\text{Phalanx}}}{N_{\text{CPU}}} \leq w_O$$

which leads to the lower bound on computational power ($N_\text{CPU}$) :

$$N_{\text{CPU}} \geq \left \lceil \frac{2^{\rho} \cdot T_{\text{grinding}}^{\text{Phalanx}}}{w_O} \right \rceil$$

1.3.1 Formula

From Section 1.1, the per-attempt grinding time under Phalanx is:

$$T_{\text{grinding}}^{\text{Phalanx}} = \frac{\rho}{2} T_{\text{BLAKE2b}} + w_T \cdot ( T_{\mathsf{VRF}} + T_{\text{eligibility}} ) + T_{\text{eval}} + T_{\Phi}$$

Substituting this into the inequality:

$$N_{\text{CPU}} \geq \left \lceil \frac{2^{\rho} \cdot \left( \frac{\rho}{2} T_{\text{BLAKE2b}} + w_T \cdot ( T_{\mathsf{VRF}} + T_{\text{eligibility}} ) + T_{\text{eval}} + T_{\Phi} \right)}{w_O} \right \rceil$$

The grinding opportunity window is:

$$\frac{X_A(w)}{f} \leq w_O \leq \frac{w}{f}$$

Assuming worst-case upper bound $w_O = \frac{w}{f}$ and noting $w < 2 \cdot \rho - 1$, we substitute:

$$N_{\text{CPU}} \geq \left \lceil f \cdot \frac{2^{\rho} \cdot \left( \frac{\rho}{2} T_{\text{BLAKE2b}} + w_T \cdot ( T_{\mathsf{VRF}} + T_{\text{eligibility}} ) + T_{\text{eval}} + T_{\Phi} \right)}{w} \right \rceil$$

Bounding $w < 2 \cdot \rho - 1$:

$$N_{\text{CPU}} \geq \left \lceil f \cdot \frac{2^{\rho} \cdot \left( \frac{\rho}{2} T_{\text{BLAKE2b}} + w_T \cdot ( T_{\mathsf{VRF}} + T_{\text{eligibility}} ) + T_{\text{eval}} + T_{\Phi} \right)}{2 \cdot \rho - 1} \right \rceil$$

Rewriting:

$$N_{\text{CPU}} \geq \left \lceil f \cdot 2^{\rho} \cdot \left( \frac{\frac{\rho}{2} T_{\text{BLAKE2b}}}{2 \cdot \rho - 1} + \frac{w_T \cdot ( T_{\mathsf{VRF}} + T_{\text{eligibility}} )}{2 \cdot \rho - 1} + \frac{T_{\text{eval}}}{2 \cdot \rho - 1} + \frac{T_{\Phi}}{2 \cdot \rho - 1} \right) \right \rceil$$

Approximating $2 \cdot \rho - 1 \approx 2 \rho$:

$$N_{\text{CPU}} > \left \lceil \frac{f}{2 \rho} \cdot 2^{\rho} \cdot \left( \rho T_{\text{BLAKE2b}} + 2 w_T \cdot ( T_{\mathsf{VRF}} + T_{\text{eligibility}} ) + 2 T_{\text{eval}} + 2 T_{\Phi} \right) \right \rceil$$

Simplified:

$$N_{\text{CPU}} > \left \lceil f \cdot 2^{\rho - 2} \cdot T_{\text{BLAKE2b}} + \frac{f \cdot 2^{\rho}}{2 \rho} \cdot \left( w_T \cdot ( T_{\mathsf{VRF}} + T_{\text{eligibility}} ) + T_{\text{eval}} + T_{\Phi} \right) \right \rceil$$

Or grouped as:

$$N_{\text{CPU}} > \left \lceil f \cdot 2^{\rho - 2} \cdot T_{\text{BLAKE2b}} + \frac{f}{\rho} \cdot 2^{\rho - 1} \cdot \left( w_T \cdot ( T_{\mathsf{VRF}} + T_{\text{eligibility}} ) + T_{\text{eval}} + T_{\Phi} \right) \right \rceil$$

1.3.2 Estimated Formula Using Mainnet Cardano Parameters

Starting from the final expression at the end of the last section:

$$N_{\text{CPU}} > \left \lceil f \cdot 2^{\rho-2} \cdot T_{\text{BLAKE2b}} + \frac{f}{\rho} \cdot 2^{\rho-1} \cdot \left( w_T \cdot ( T_{\mathsf{VRF}} + T_{\text{eligibility}} ) + T_{\text{eval}} + T_{\Phi} \right) \right \rceil$$

Using Cardano’s mainnet values:

• $T_{\mathsf{VRF}} = 10^{-6}$ seconds (1 microsecond) – Time to evaluate a Verifiable Random Function.
• $T_{\text{BLAKE2b}} = 10^{-8}$ seconds (0.01 microseconds) – Time for a BLAKE2b-256 hash operation.
• $f = \frac{1}{20} = 0.05$ – Active slot coefficient.
• $k = 2160$
• Slot duration = 1 second.

Since the eligibility check is negligible, set $T_{\text{eligibility}} \approx 0$:

Substitute into the expression:

• First term:

  $$f \cdot 2^{\rho-2} \cdot T_{\text{BLAKE2b}} = 0.05 \cdot 2^{\rho-2} \cdot 10^{-8} = 5 \cdot 10^{-10} \cdot 2^{\rho-2}$$

• Second term:

  $$\frac{f}{\rho} \cdot 2^{\rho-1} \cdot \left( w_T \cdot 10^{-6} + T_{\text{eval}} + T_{\Phi} \right) = \frac{0.05 \cdot 2^{\rho-1}}{\rho} \cdot \left( 10^{-6} w_T + T_{\text{eval}} + T_{\Phi} \right)$$

The estimated number of CPUs required is:

$$N_{\text{CPU}} > \left \lceil 5 \cdot 10^{-10} \cdot 2^{\rho - 2} + \frac{5 \cdot 10^{-8} \cdot 2^{\rho - 1}}{\rho} \cdot w_T + \frac{5 \cdot 10^{-2} \cdot 2^{\rho - 1}}{\rho} \cdot T_{\text{eval}} + \frac{5 \cdot 10^{-2} \cdot 2^{\rho - 1}}{\rho} \cdot T_{\Phi} \right \rceil$$

1.3.3 Impact of Tᵩ on Canonical Scenarios

Now that we have an updated formula, we can evaluate how Phalanx directly affects the cost of grinding attempts when compared to the original CPD scenarios. As previously discussed, the goal is to strike a balance between the effort expected from honest SPOs during an epoch and the computational burden imposed on an adversary attempting to evaluate multiple $`\eta_e`$ candidates in preparation for an attack.

To anchor this analysis, we introduce a baseline configuration denoted as $`\text{Phalanx}_\text{1/100}`$: an overhead equal to 1/100 of an epoch, corresponding to $432{,}000 \div 100 = 4{,}320$ slots. This represents a modest but meaningful choice — substantial enough to raise the adversary’s cost significantly, yet conservative enough to avoid overloading honest participants. In contrast, imposing a full-epoch overhead would likely be excessive in practice, potentially destabilizing the protocol or placing undue demands on block producers. We may refer to that upper bound as $`\text{Phalanx}_{\text{max}}`$, and the present section aims to explore and recommend a viable configuration somewhere between this maximum and our conservative baseline.

Since each slot lasts 1 second, the $`\text{Phalanx}_\text{1/100}`$ overhead equates to 4,320 seconds, or exactly 1 hour and 12 minutes.

We now revisit the canonical scenarios from CPD Section 3.5 – Scenarios, and extend each one with a Phalanx-enhanced variant that incorporates this fixed computational cost: $`T_{\Phi} = 4320 \, \text{seconds}`$. The resulting $N_{\text{CPU}}$ formulas are derived by substituting each scenario’s respective values for $`w_T`$ and $`T_{\text{eval}}`$ into the base expression from Section 1.2.2, now augmented with the constant Phalanx term $`T_{\Phi}`$.

$$N_{\text{CPU}} > \left \lceil 5 \cdot 10^{-10} \cdot 2^{\rho - 2} + \frac{5 \cdot 10^{-8} \cdot 2^{\rho - 1}}{\rho} \cdot w_T + \frac{5 \cdot 10^{-2} \cdot 2^{\rho - 1}}{\rho} \cdot T_{\text{eval}} + \frac{216 \cdot 2^{\rho - 1}}{\rho} \right \rceil \quad \text{(Phalanx}_\text{1/100}\text{)}$$ $$N_{\text{CPU}} > \left \lceil 5 \cdot 10^{-10} \cdot 2^{\rho - 2} + \frac{5 \cdot 10^{-8} \cdot 2^{\rho - 1}}{\rho} \cdot w_T + \frac{5 \cdot 10^{-2} \cdot 2^{\rho - 1}}{\rho} \cdot T_{\text{eval}} \right \rceil \quad \text{(Praos)}$$

The table below summarizes the expressions for each scenario:

Scenario	$\text{Praos}$	$\text{Phalanx}_\text{1/100}$
Ant Glance	$5 \cdot 10^{-10} \cdot 2^{\rho-2}$	$5 \cdot 10^{-10} \cdot 2^{\rho-2} + 216 \cdot \frac{2^{\rho-1}}{\rho}$
Ant Patrol	$5 \cdot 10^{-10} \cdot 2^{\rho-2} + 2.16 \cdot 10^{-2} \cdot \frac{2^{\rho-1}}{\rho}$	$5 \cdot 10^{-10} \cdot 2^{\rho-2} + 2.16 \cdot 10^{-2} \cdot \frac{2^{\rho-1}}{\rho} + 216 \cdot \frac{2^{\rho-1}}{\rho}$
Owl Stare	$5 \cdot 10^{-10} \cdot 2^{\rho-2} + 5 \cdot 10^{-2} \cdot \frac{2^{\rho-1}}{\rho}$	$5 \cdot 10^{-10} \cdot 2^{\rho-2} + 5 \cdot 10^{-2} \cdot \frac{2^{\rho-1}}{\rho} + 216 \cdot \frac{2^{\rho-1}}{\rho}$
Owl Survey	$5 \cdot 10^{-10} \cdot 2^{\rho-2} + 7.16 \cdot 10^{-2} \cdot \frac{2^{\rho-1}}{\rho}$	$5 \cdot 10^{-10} \cdot 2^{\rho-2} + 7.16 \cdot 10^{-2} \cdot \frac{2^{\rho-1}}{\rho} + 216 \cdot \frac{2^{\rho-1}}{\rho}$

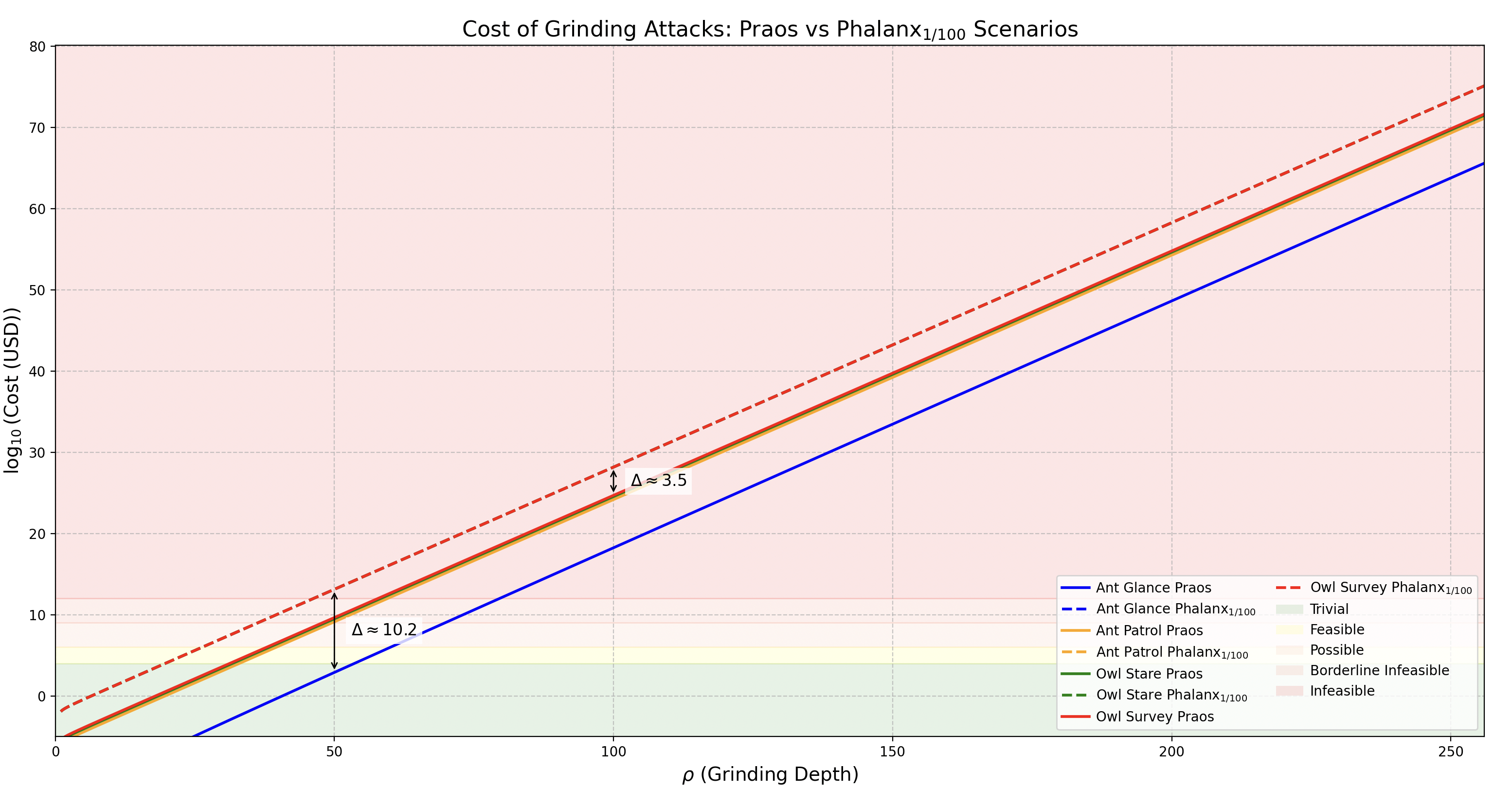
The graph below presents the logarithmic cost (in USD) of executing grinding attacks as a function of the grinding depth ($`\rho`$), across both Praos and $\text{Phalanx}_{1/100}$ scenarios.

• Solid lines correspond to the original Praos configurations (Ant Glance, Ant Patrol, Owl Stare, and Owl Survey).
• Dashed lines represent the respective $\text{Phalanx}_\text{1/100}$ variants, each incorporating a fixed additional computational overhead of $`T_{\Phi} = 4320 \, \text{seconds}`$.
• The shaded feasibility regions reflect increasing economic difficulty levels, based on thresholds defined in CPD Section 3.6 – Grinding Power Computational Feasibility.

✏️ Note: The Python script used to generate this graph is available here ➡️ scenario_cost_praos_vs_phalanx.py

The graph highlights how the $\text{Phalanx}_\text{1/100}$ protocol dramatically increases the cost of grinding attacks compared to Praos, using a logarithmic scale to represent costs in USD as a function of the grinding depth $`\rho`$:

1. Consistent Cost Increase Across All $\rho$ Values The differences (deltas) between $\text{Phalanx}_\text{1/100}$ and Praos scenarios remain stable across all grinding depths due to the logarithmic scale. This allows us to make generalizable observations regardless of $\rho$.

2. Moderate Gap Between Scenarios Within $\text{Phalanx}_\text{1/100}$ Variations between different $\text{Phalanx}_\text{1/100}$ scenarios (e.g., Ant Glance vs Owl Survey) are relatively modest. For example:

   • At $`\rho = 100`$, the cost difference between Owl Survey ($\text{Phalanx}_\text{1/100}$) and Owl Survey (Praos) is about 3.5 orders of magnitude in $`\log_{10}(\text{Cost})`$.

3. Significant Overhead Introduced by $\text{Phalanx}_\text{1/100}$ The computational burden imposed by Phalanx is substantial.

   • At $`\rho = 150`$, the cost delta between Owl Survey ($\text{Phalanx}_\text{1/100}$) and Ant Glance (Praos) reaches nearly 9.8, representing a 10⁹.⁸× increase in expected cost for the attacker.
   • This effectively pushes grinding attacks into the "infeasible" zone for a wide range of strategies.

4. Strategic Uniformity Under $\text{Phalanx}_\text{1/100}$ All $\text{Phalanx}_\text{1/100}$ scenario curves tightly cluster together, showing minimal divergence across evaluation complexity ($T_{\text{eval}}$) and observation scope ($w_T$).

   • This implies that Phalanx equalizes grinding costs across adversarial strategies.
   • Practically, this means defenders (e.g., protocol designers) can reason about attack feasibility without considering specific adversarial tactics. One cost curve is sufficient.

We can now simplify and generalize the grinding cost formulas for different Phalanx configurations, along with their estimated order-of-magnitude improvements over Praos:

Configuration	Time Budget	Grinding Cost Formula	Cost Amplification
$`\text{Phalanx}_{1/100}`$	2 hours	$`\frac{2.16 \cdot 10^{2} \cdot 2^{\rho - 1}}{\rho}`$	$\boldsymbol{10^{10.2}}$×
$`\text{Phalanx}_{1/10}`$	12 hours	$`\frac{2.16 \cdot 10^{3} \cdot 2^{\rho - 1}}{\rho}`$	$\boldsymbol{10^{11.2}}$×
$`\text{Phalanx}_{\text{max}}`$	5 days	$`\frac{2.16 \cdot 10^{4} \cdot 2^{\rho - 1}}{\rho}`$	$\boldsymbol{10^{12.2}}$×

N.B. We can note that even with the use of ASICs, with a speed up of 3x to 10x, Phalanx would still add a significant term and reduce the cost amplification to still acceptable levels.

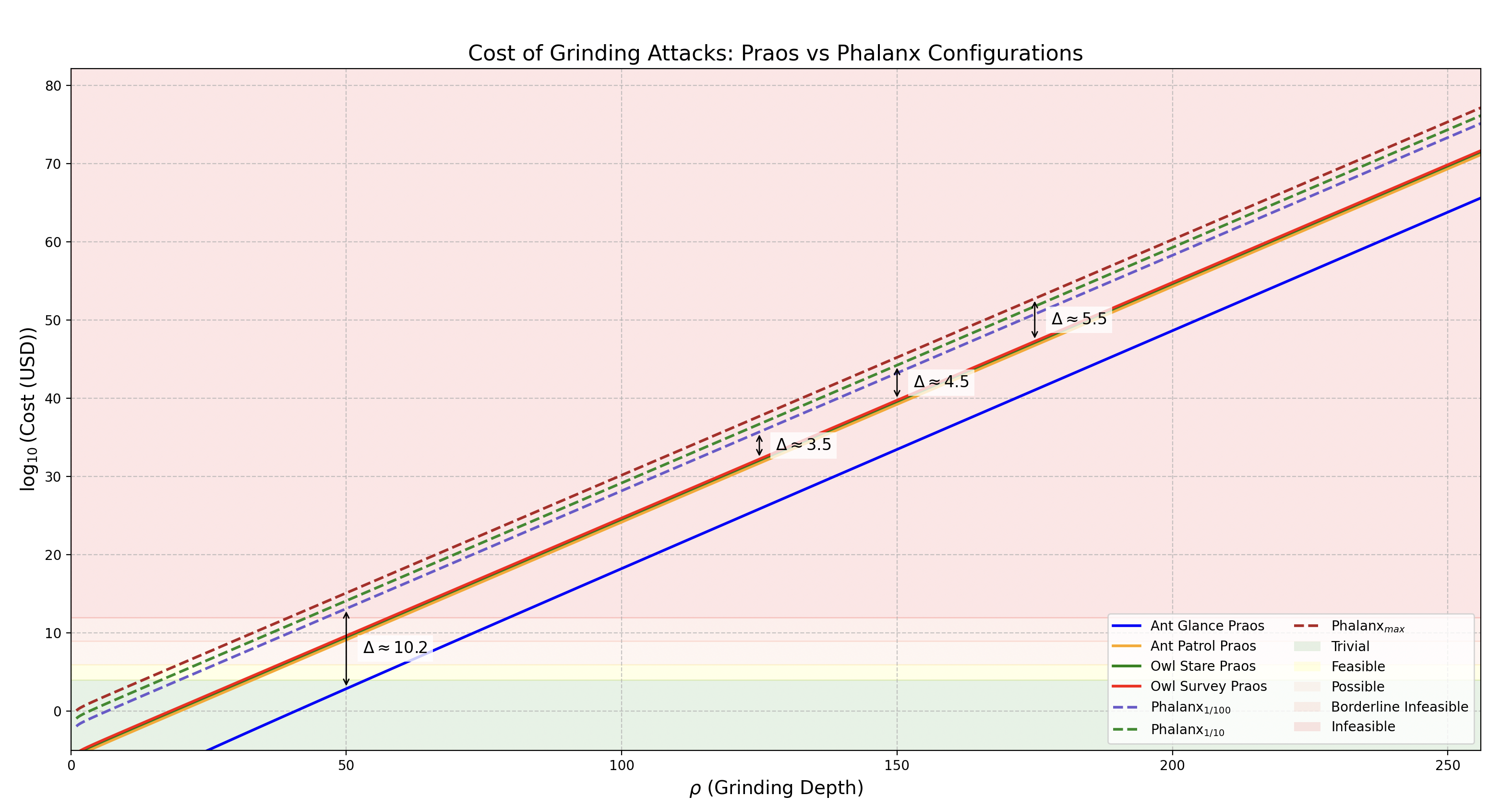
✏️ Note: The Python script used to generate this graph is available here ➡️ scenario_cost_praos_vs_phalanx-full-scenarios.py.

These results confirm that even the minimal configuration ($`\text{Phalanx}_{1/100}`$) yields a $10^{10.6}$-fold increase in the computational cost of a grinding attack — a formidable barrier for adversaries. More aggressive deployments such as $`\text{Phalanx}_{1/10}`$ and $`\text{Phalanx}_{\text{max}}`$ push this cost further, to $10^{11.6}$ and $10^{12.6}$ times that of Praos, respectively — while still remaining practical for honest participants.

1.3.4 Impact of Tᵩ on Feasibility Categories

This simplification allows us to revisit and improve the feasibility category table presented in the Problem Overview section :

✏️ Note: The code to generate this graph is available at ➡️ this link.

The tables below present first the original Praos feasibility intervals, followed by the adjusted categories under Phalanx :

Feasibility Category	🔵 Ant Glance	🟠 Ant Patrol	🟢 Owl Stare	🔴 Owl Survey	$`\text{Phalanx}_{1/100}`$	$`\text{Phalanx}_{1/10}`$	$`\text{Phalanx}_{max}`$
🟢 🌱 Trivial for Any Adversary	$`0 \to 53.6`$	$`0 \to 32.9`$	$`0 \to 31.6`$	$`0 \to 31.1`$	$`0 \to 19.6`$	$`0 \to 16.3`$	$`0 \to 13.0`$
🟡 💰 Feasible with Standard Resources	$`53.6 \to 60.0`$	$`32.9 \to 39.5`$	$`31.6 \to 38.3`$	$`31.1 \to 37.8`$	$`19.6 \to 26.3`$	$`16.3 \to 23.0`$	$`13.0 \to 19.6`$
🟠 🏭 Large-Scale Infrastructure Required	$`60.0 \to 69.7`$	$`39.5 \to 49.5`$	$`38.3 \to 48.2`$	$`37.8 \to 47.7`$	$`26.3 \to 36.2`$	$`23.0 \to 32.9`$	$`19.6 \to 29.6`$
🔴 🚫 Borderline Infeasible	$`69.7 \to 79.4`$	$`49.5 \to 59.5`$	$`48.2 \to 58.2`$	$`47.7 \to 57.7`$	$`36.2 \to 46.2`$	$`32.9 \to 42.9`$	$`29.6 \to 39.5`$
🔴 🚫 Infeasible	$`79.4 \to 256`$	$`59.5 \to 256`$	$`58.2 \to 256`$	$`57.7 \to 256`$	$`46.2 \to 256`$	$`42.9 \to 256`$	$`39.5 \to 256`$

The Phalanx tables include delta improvements for each Praos scenario. A positive $\Delta$ implies that Phalanx forces infeasibility earlier, i.e., at a lower $`\rho`$ value, thereby increasing adversarial cost :

Scenario	$`\Delta \text{Phalanx}_{1/100}`$	$`\Delta \text{Phalanx}_{1/10}`$	$`\Delta \text{Phalanx}_{max}`$
🔵 Ant Glance	$`+34.0`$	$`+36.5`$	$`+39.9`$
🟠 Ant Patrol	$`+13.3`$	$`+16.6`$	$`+20.0`$
🟢 Owl Stare	$`+12.0`$	$`+15.3`$	$`+18.7`$
🔴 Owl Survey	$`+11.5`$	$`+14.8`$	$`+18.2`$

1.4 Conclusion: How Much Risk is Mitigated?

To quantify the security improvement, we compute the percentage reduction in the “Trivial for Any Adversary” interval compared to Praos. This represents the portion of grinding attacks that are now pushed into more difficult feasibility regions.

Scenario	Praos Trivial	$`\Delta \text{Phalanx}_{1/100}`$	% Reduction	$`\Delta \text{Phalanx}_{1/10}`$	% Reduction	$`\Delta \text{Phalanx}_{max}`$	% Reduction
🔵 Ant Glance	53.6	19.6	−63.4%	16.3	−69.6%	13.0	−75.7%
🟠 Ant Patrol	32.9	19.6	−40.4%	16.3	−50.5%	13.0	−60.5%
🟢 Owl Stare	31.6	19.6	−38.0%	16.3	−48.4%	13.0	−58.9%
🔴 Owl Survey	31.1	19.6	−37.0%	16.3	−47.6%	13.0	−58.2%

These results show that Phalanx makes low-effort grinding substantially harder, reducing adversarial opportunity for trivial manipulation by up to 76% in the most favorable configuration, and by at least 37% across all attack types and parameterizations.

This concludes our high-level assessment of feasibility mitigation in security terms. In the next section, “2. How Phalanx Improves CPS-17 – Settlement Speed?”, we will examine how this risk reduction translates into a much more tangible and practical benefit: faster and more reliable settlement times in Ouroboros.

2. How Phalanx Improves CPS-17 - Settlement Speed?

Let us recall that, like Bitcoin, Cardano relies on probabilistic and unbiased randomness for leader election. As a result, both systems inherently provide statistical consensus guarantees. For Stake Pool Operators (SPOs), being elected as a slot leader grants some control over the protocol. This control increases with stake—more skin in the game means more chances to be selected. However, due to the randomized nature of the leader election, SPOs cannot predict or influence exactly when they will be selected.

This makes undesirable events—such as regional concentrations of slot leadership deviating from the expected distribution, or control over multiple consecutive blocks—statistically quantifiable and, in the absence of grinding attacks, extremely unlikely. These include risks like rollbacks, $k$-common prefix violations, or private chain attacks. This is precisely the security model Ouroboros Praos was designed around—and so far, it has held up well.

However, if adversaries manage to control more than 20% of the stake, they gain significant and exponentially growing grinding power. This power allows them to bend the statistical distribution of events in their favor. For example, achieving a grinding depth of 79.4 means they can select from among $2^{79.4}$ (~ $10^{24}$) possible distributions to optimize the timing and nature of their attacks. At that scale, they can deliberately amplify the probability of "bad events" and execute a variety of targeted attacks against the protocol.

In this section, we narrow our focus to a specific class of such bad events: those that bias or delay the confirmation time of transactions on Cardano. We’ll show how this issue is directly tied to adversarial grinding power, and how reducing that power leads to faster and more reliable settlement guarantees, thereby directly addressing CPS-0017 / Settlement Speed.

2.1 Settlement times without grinding attacks

In longest-chain consensus protocols like Ouroboros Praos, settlement time refers to the duration required for a transaction to be considered irreversibly included in the blockchain with high probability. Without grinding attacks, this is primarily determined by the risk of chain reorganizations (e.g., forks or common prefix violations), where an adversary might create a competing chain that overtakes the honest one. The goal is to compute the minimum number of confirmations (blocks appended after the transaction's block) needed to achieve a target security level, such as a failure probability below $2^{-30}$ or $2^{-60}$.

The methodology for computing settlement bounds, as detailed in the paper "Practical Settlement Bounds for Longest-Chain Consensus" (Gaži et al., 2022), uses a phase-based analytical model that divides time into intervals separated by the maximum network delay $\Delta$ (e.g., 2-5 seconds for Cardano). It tracks metrics like "margin" (for PoW) or "reach" and "margin" (for PoS) to bound the probability of an adversary overtaking the honest chain.

To obtain metrics, you can run the software from https://github.com/renling/LCanalysis/, which implements these evaluations in MATLAB. Clone the repo, open PoSRandomWalk.m (for PoS like Cardano), set parameters (e.g., honest ratio $\beta = 0.7$ (30% of stake adversary), network delay $\Delta = 5s$), and run to output failure probabilities vs. confirmations. Below is a representative graph:

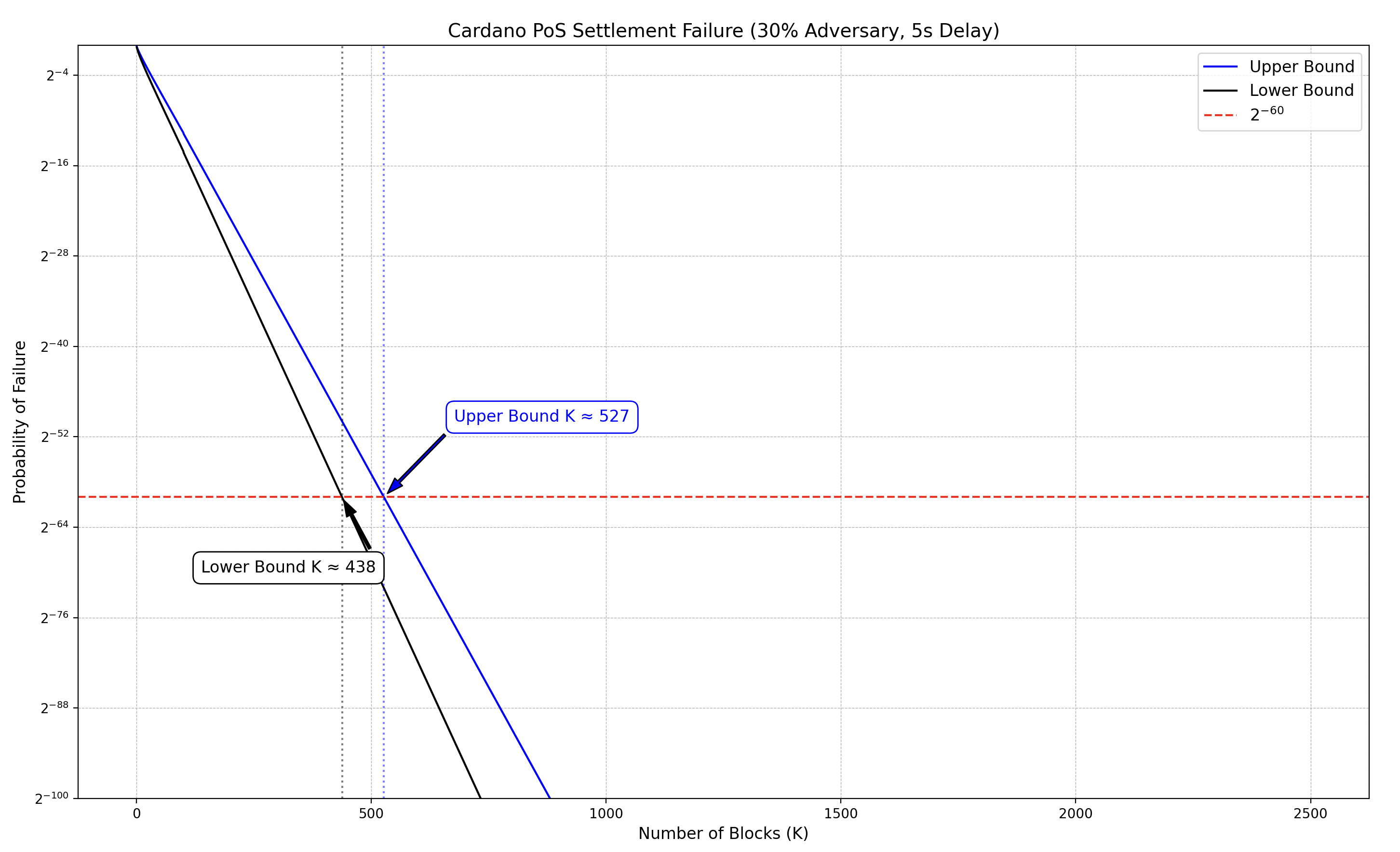
✏️ Note: The Python script used to generate this graph is available here ➡️ settlement-time-without-grinding.py.

A 60-bit confidence level (failure probability ≤ $2^{-60}$) is a common threshold where events are considered negligible in practice. In the graph above, for example, this corresponds to a confirmation interval of [438, 527] blocks. Beyond this, the choice of confidence level and thus the number of confirmations required for transaction settlement, becomes application-specific, balancing security against efficiency.

2.2 How Grinding Power Affects Settlement Times

What does it mean for settlement times when, in a scenario like the Owl Survey Glance, the adversary can observe a large portion of the candidate randomness distribution and perform an attack with a grinding power of $2^{57.7}$?

A grinding power of $2^{57.7}$ / a grinding depth of 57.7 bits, implies that:

• The adversary can simulate approximately $2^{57.7}$ distinct randomness outcomes, derive the associated leader schedules for the next epoch, and select the most favorable one.
• This drastically increases the likelihood of bad events (e.g., settlement failures) compared to a protocol with unbiased randomness.
• More precisely, if a bad event occurs with probability $\varepsilon$ under honest randomness, then an adversary capable of evaluating $R$ different randomness candidates can amplify this probability up to $R \cdot \varepsilon$ (by the union bound).

In practical terms, such grinding power extends the number of confirmations required to reach a desired security level. The stronger the adversary’s grinding capability, the longer it takes for a transaction to be considered truly settled.

For example, assume that on mainnet, a rollback probability of $2^{-60}$ is achieved for a block at index $x$ after $y$ subsequent blocks are appended. If an adversary possesses grinding power of $2^{57.7}$, the effective risk increases to:

$$2^{-60} \cdot 2^{57.7} = 2^{-2.3}$$

To preserve the original $2^{-60}$ confidence level under adversarial grinding, the protocol must instead target a baseline security of:

$$2^{-(60 + 57.7)} = 2^{-117.7}$$

This implies that many more blocks must be appended before a block is considered settled, thereby significantly increasing settlement times.

In the example above, we used the Owl Survey Glance scenario, which is the most computationally expensive in terms of grinding cost. However, when establishing a protocol-wide security threshold, it is more prudent to anchor on the worst-case grinding power — that is, the scenario with the highest grinding depth. In our analysis, this is the Ant Glance scenario, with a grinding depth of 79.4 bits. To maintain the original $2^{-60}$ confidence level under such an adversary, the protocol must instead target:

$$2^{-(60 + 79.4)} = 2^{-139.4}$$

This defines a stricter baseline and ensures security even against the most favorable conditions for the adversary. In our previous scenario (30% adversary and 5-second network delay), the effect can be visualized as follows:

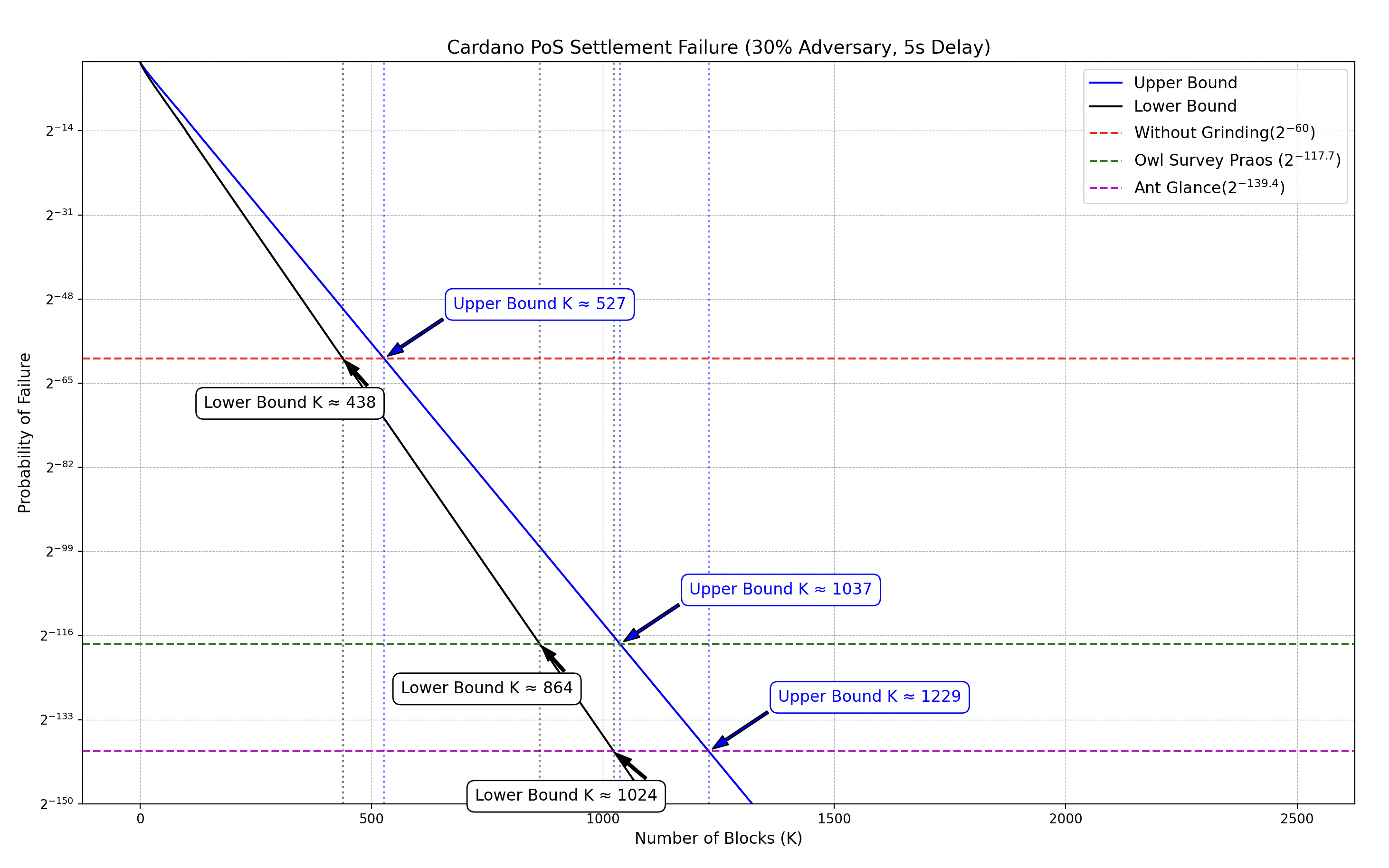
✏️ Note: The Python script used to generate this graph is available here ➡️ settlement-time-praos.py.

Where the confirmation interval was [438, 527] blocks in the absence of a grinding attack, it increases to [864, 1037] blocks under grinding power $2^{57.7}$ in the Owl Survey scenario, and further to [1024, 1229] blocks under the same grinding power in the Ant Glance scenario.

Assuming a block is produced every 20 seconds, this extends the required confirmation window from approximately [2.43, 2.93] hours to [4.80, 5.76] hours in the Owl Survey case, and up to [5.69, 6.83] hours in the Ant Glance case — more than doubling the settlement time.

As discussed in Section 1: How Phalanx Addresses CPS-21 – Ouroboros Randomness Manipulation, this is a key challenge in Praos: the presence of multiple attack scenarios with varying grinding power makes it difficult to define a single, consistent security threshold for settlement — a complexity that Phalanx simplifies by unifying the treatment of adversarial power across scenarios.

2.3 How Phalanx improves compared to Praos ?

In the conclusion of Section 1.4: How Much Risk Is Mitigated?, we quantified Phalanx's improvement over Praos in terms of grinding depth reduction as follows:

Scenario	$`\Delta \text{Phalanx}_{1/100}`$	$`\Delta \text{Phalanx}_{1/10}`$	$`\Delta \text{Phalanx}_{\text{max}}`$
🔵 Ant Glance	$`+34.0`$	$`+36.5`$	$`+39.9`$

In our previous examples, we are given that under Praos, the Ant Glance scenario results in a required security level of $`2^{-139.4}`$, which translate into the following threshold for the Phalanx configurations :

Configuration	Computation	Resulting Security Level
$`\text{Phalanx}_{1/100}`$	$2^{-139.4 + 34.0}$	$2^{-105.4}$
$`\text{Phalanx}_{1/10}`$	$2^{-139.4 + 36.5}$	$2^{-102.9}$
$`\text{Phalanx}_{\text{max}}`$	$2^{-139.4 + 39.9}$	$2^{-99.5}$

This can be visualized as follows:

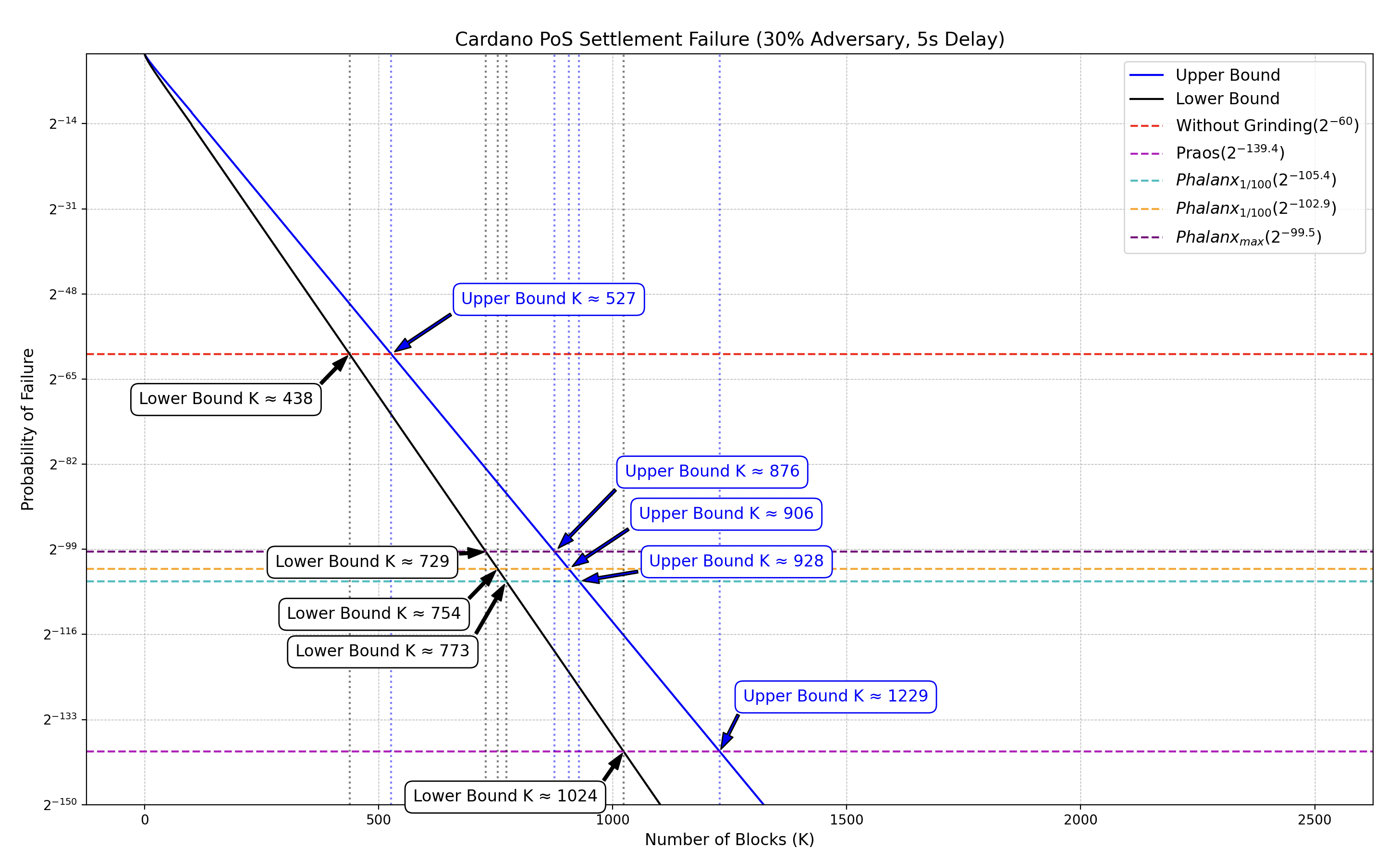
✏️ Note: The Python script used to generate this graph is available here ➡️ settlement-time-phalanx.py.

In the absence of a grinding attack, the confirmation interval was [438, 527] blocks. Under the actual version of Praos, accounting for a grinding depth of 79.4 bits in the Ant Glance scenario, this interval increases to [1024, 1229] blocks.

However, with Phalanx applied, the required confirmation windows are significantly reduced:

Configuration	Confirmation Interval	Duration @ 20s/block
$`\text{Phalanx}_{1/100}`$	[773, 928]	~4.29 h → ~5.16 h
$`\text{Phalanx}_{1/10}`$	[754, 906]	~4.19 h → ~5.03 h
$`\text{Phalanx}_{\text{max}}`$	[729, 876]	~4.05 h → ~4.87 h

Compared to Praos' ~5.69 h → ~6.83 h (from blocks 1024 to 1229), these configurations reduce settlement time by approximately 20–30% while maintaining equivalent security.

2.4 Advocating for Peras: Phalanx as a Complementary Layer

Ouroboros Peras is a recent protocol extension designed to accelerate settlement in Cardano by introducing stake-weighted voting and certified blocks. Built as a lightweight augmentation of Praos, it enables rapid finality—often within 1 to 2 minutes—by allowing randomly selected committees to vote on blocks and issue certificates that elevate their importance in the chain selection rule (Peras Intro). Critically, Peras maintains full compatibility with Praos' security guarantees, reverting gracefully when quorum is not reached (Peras FAQ). Rather than replacing Praos, it overlays an additional mechanism for fast, probabilistically final settlement, offering a much-needed middle ground between immediate confirmation and the traditional 2160-block security window.

While Peras dramatically reduces settlement times compared to both Praos and Phalanx, it does so through a certification mechanism that depends on the timely participation of randomly selected committees. In practice, this mechanism offers fast settlement when quorum is achieved—but when participation conditions are not met (e.g., insufficient online stake or network asynchrony), Peras gracefully falls back to standard Praos behavior (Peras Technical Report). This fallback mode retains the full settlement guarantees we've detailed in this CIP and in the accompanying CPS-18: Ouroboros Randomness Manipulation and CIP-Phalanx. In such scenarios, settlement times revert to those defined under grinding-aware Praos parameters—precisely where Phalanx becomes relevant as a complementary defense layer, ensuring that even in fallback conditions, the chain benefits from stronger security guarantees and significantly improved settlement times compared to unmodified Praos.

Finally, a point of critical importance that we emphasized in the CPS-21: Ouroboros Randomness Generation Sub-Protocol – The Coin-Flipping Problem: today, the protocol remains effectively blind to grinding attacks. Within the window of opportunity defined in the CPD, detecting randomness manipulation is inherently difficult—both in terms of real-time monitoring and retrospective analysis. However, Ouroboros Peras introduces a meaningful defense: by reducing settlement times to 1–2 minutes (Peras FAQ), it can close the grinding window entirely, provided it does not fall back to Praos mode during this period. If such a fallback does occur within the grinding window, it becomes a suspicion that a grinding attempt may be underway. In this case, examining which SPOs abstained from voting during the certification phase could provide actionable insights to identify adversarial behavior. In this light, Peras is not only a mechanism for faster settlement—it also contributes to resilience against randomness manipulation.

We therefore strongly recommend deploying both mechanisms in tandem:

• Peras for rapid probabilistic finality and real-time detection,
• Phalanx as a fallback that offers quantifiable grinding resistance even in worst-case epochs.

Note: If Peras committee selection ultimately relies on randomness from the standard beacon in its production version, it too inherits vulnerability to grinding — especially when a Praos epoch precedes a Peras epoch. In such cases, Phalanx mitigates the grinding risk at the source, reducing the manipulation surface of the beacon and thereby indirectly strengthening Peras. This highlights the complementarity of the two systems: each reinforces the other.

3. Why VDFs Were Chosen over other Cryptographic Primitives ?

As shown previously in the CPS and CPD, Cardano’s randomness generation currently is biasable and this CIP aims at presenting solutions on top of the current Praos’ randomness generation algorithm to disincentivize adversaries from performing grinding attacks by increasing their computational cost. We do not intend to change the protocol in depth, as this would need a much greater initiative that may not bear fruits, but add an additional layer of security on top of the current protocol only.

To argue about our decision, i.e. increasing the attack cost, we first list different ways to fix the last revealer attack as suggested in 1 that present a similar issue when combining different sources of randomness.

• Simultaneous lottery draws, so that all random nonces are revealed at once. Unfortunately this solution is not possible in our context as nonces are revealed iteratively in block headers so that they can be easily extractable and verifiable from the blockchain directly.
• Using a slow function to generate the randomness on top of the revealed nonces, so that the adversary cannot decide in time whether to reveal their nonces or not. In practice, time assumptions are delicate in cryptography for theoretical reasons (potential attacks, better algorithms) and practical ones (Moore’s law).
• Using a commitment, so that the revealed nonces are combined to some previously committed value. This solution is not feasible as we would either need to rely on trusted parties, which is contrary to blockchain’s operandi, or to reveal the committed values, which is equivalent to RANDAO.
• Limiting the entropy of the last lottery draws, by combining it with sufficiently many low entropy - a single bit- randomness. This solution is impractical as we would still have a revealer attack, but on the lone bits.

As such, we should focus from now on using a weakened slow function, that is instead of solely relying on time based guarantees, we will principally count on computational costs: we will append to our existing protocol a computationally costly chain of computation that the adversary will have to process for each grinding attempt.

3.1 Requirements

When choosing a cryptographic primitive, we need to balance several criteria. In particular, checking its security strength and maturity, performance, deployability and compliance:

• Security strength & Maturity: the primitive is resistant to known attacks and comprise a sufficient security margin. Furthermore, it has been extensively reviewed by the cryptographic community, has been developed transparently and has been accepted and standardized.
• Performance: the primitive is efficient in terms of size (input, output and if applicable proof size), and computation (CPU cycles, memory footprint, and power consumption) with respect to the application and intended platform.
• Deployability: the primitive should be easy to set up, upgrade and, in case of attacks and if possible, switch
• Compliance: the primitive should be free of licensing restrictions and meet regulatory standards.

We furthermore require the following properties for the Phalanx project. The cryptographic primitive must be an NP deterministic function. More precisely, a primitive whose verification time is fast, that for each input corresponds to a unique output and whose latter is fixed.

We can either support a primitive which computation can be split in different iterations, each of which is verifiable, or which is finely tunable so that we can solve a challenge in less than a block time and can be used in cascade. Being able to generate and verify a single proof for the whole chain of computation would be another advantage in the context of syncing.

3.2 Primitive selection

To ensure fast verification, we face a first choice: relying on a cryptographic primitive based on trapdoor assumptions, which present NP problems and by definition have fast verification, or combine a primitive without fast verification with an efficient proof system such as a Succinct Non-interactive ARgument of Knowledge (SNARK).

3.2.1 RSA solutions

An RSA group is the multiplicative group of integers modulo $N$, where $N$ is the product of two large prime numbers $p$ and $q$, $N = p \cdot q$. This group is called RSA after the RSA cryptosystem by Rivest, Shamir and Adleman where the public encryption key is the group modulus $N$ and a small exponent $e$, while the corresponding decryption key is the number $d$ such that $d \cdot e \equiv 1\ (\text{mod }\Phi(N))$ where $\Phi(N) = (p−1)(q−1)$, where $p$ and $q$ remain private. To break the RSA cryptosystem, the adversary has to factorize $N$ into its prime $p$ and $q$ which can be done most efficiently with the General Number Field Sieve algorithm, based on the NFS [2], in sub-exponential time. To reach 128 bit of security, the modulus must be at least 2,048 bit long, and preferably at least 3,072 bit long, according to NIST [3].

3.2.1.1 Designs

Three problems defined on RSA groups satisfy the requirements: solving the RSA problem or the integer factorization, or using verifiable delayed functions (VDFs, [6]). RSA problem. The setup consists in generating an RSA public key $(N,\ e)$ where $N$’s factorization is unknown and a ciphertext c. The challengers then have to find the plaintext corresponding to that ciphertext, that is finding the eth root the ciphertext modulo N, i.e. finding $m$ such that $c \equiv m \cdot e (\text{mod } N)$. The verification is straightforward, re-encrypting the plaintext and checking it equals the ciphertext. The most efficient method to solve this problem is by first factoring the modulus $N$, which cannot be done in polynomial time without a quantum computer (in which case we would use Shor’s algorithm). The best published algorithm to solve this problem with classical computers is the general number field sieve (GNFS), that is sub-exponential in time. Integer factorization. This is a simpler case to the RSA problem: only the group modulus is given and needs to be factorized, by the same algorithm. VDF. Similarly to the other problems, we first start by generating an unknown order group of modulus $N$ but also sample a random group element $g$. The challenge then consists in raising this element to a big exponent of the form $2^T$ where $T$ is set depending on the difficulty, the computation or time we want the challenger to need to solve the problem. The challengers eventually compute and output $y = x^{2^T} (\text{mod }N)$ by squaring the integer $x$ exactly $T$ times as well as generate an additional proof of this result. The verification consists in verifying the proof passes successfully together with the input, output and modulus.

3.2.1.2 Properties

Security Strength & Maturity. RSA cryptography, since its introduction in 1977, has reached a high level of maturity and is widely considered one of the most reliable and well-understood public-key cryptographic systems. Its security is based on the computational difficulty of factoring large composite numbers, a problem that has remained challenging even with significant advances in both hardware and algorithmic techniques. Over the years, RSA has undergone extensive cryptanalysis, making it one of the most scrutinized cryptographic algorithms. Its applications have become deeply embedded in a wide range of security protocols, such as SSL/TLS for secure communications, digital signatures, and encryption. RSA is however vulnerable to quantum attacks; when large-scale quantum computers become practical, RSA’s security could be broken by quantum algorithms like Shor's algorithm, making it less future-proof compared to post-quantum cryptographic algorithms.

Performance. One of the main drawbacks of the RSA cryptosystem relies on its inefficiency due to large modulus, making the group element large space-wise and operations computationally expensive.

Deployability. As solving the RSA problem or integer factorization consists in breaking the group security, groups latter cannot be continuously reused in this scenario. More particularly, after finding the factorization of the group modulus, decrypting further ciphertexts in the same group becomes trivial. As for solving a VDF puzzle, the group can be reused safely as long as the modulus is of sufficient size, at least 2,048 bit-long. We can in that scenario choose a known secure modulus, whose factorization is unknown, such as an RSA challenge to create a group. Such trusted unknown moduli are however limited in numbers and we would have to generate new ones, in a trustless manner, when updating security parameters or in case of an, potentially post-quantum, attack. In our context, setting up RSA groups would be challenging to say the least, as we would need to generate groups of unknown order, that is the RSA modulus must be public while the underlying prime numbers must remain unknown. There is no known method to generate such groups, even inefficiently, which becomes especially critical if we have to do it repeatedly. Generating such a group might be achievable via multi-party computation (MPC) where the network would compute random numbers passing distributive primality tests. This would however be highly impractical.

Compliance. RSA is compliant with a wide range of security standards and regulations. It is one of the most widely accepted public-key cryptosystems and has been incorporated into many cryptographic protocols, including SSL/TLS for secure web communication, digital signatures, and email encryption. RSA complies with industry standards such as FIPS 186-4, X.509, PKCS#1 and NIST guidelines. None of the methods, GNFS or VDFs, are proprietary and there exists open source code implementing these.

3.2.2 ECC solutions

Elliptic Curve Cryptography (ECC) is a form of public-key cryptography based on the mathematical structure of elliptic curves over finite fields. More particularly, ECC relies on a safe subgroup of elliptic curves, usually defined on a prime field for security and efficiency. It provides strong security with smaller key sizes compared to traditional methods like RSA, needing 256 to 388 bit long prime only [3], making it ideal for constrained environments. To break ECC, one has to compute the discrete logarithm of the group (ECDLP), which can be done most efficiently with Pollard's Rho algorithm that solves the discrete logarithm in $\mathcal{O}(n​^{1/2})$ time and $\mathcal{O}(1)$ space.

3.2.2.1 Designs

The main problem satisfying our requirements is solving the discrete logarithmic on a secure subgroup of an elliptic curve. In that case, the setup consists in generating a curve and generator $G$, and sampling a random point $P$ from its secure subgroup. The challengers then have to find the scalar a such that $P = a \cdot G$. Verification is also straightforward, as it consists in raising $G$ to the power $a$ and verifying it equals $P$. The most efficient methods to find this scalar include the Index Calculus and Pollard’s $\rho$.

3.2.2.2 Properties

Security Strength & Maturity. Elliptic Curve Cryptography has reached a high level of maturity over the past few decades and is widely regarded as a modern, efficient alternative to traditional public-key cryptosystems like RSA. Its security is based on the hardness of the Elliptic Curve Discrete Logarithm Problem (ECDLP), which has been extensively analyzed, making ECC a trusted and well-understood cryptographic method. ECC is now widely adopted in industry standards, including TLS, SSH, Cardano, Bitcoin, and other blockchain technologies, where its efficiency and robustness are critical. ECC is also vulnerable to post-quantum attacks and can be broken in polynomial time with Pollard's Rho or the Index Calculus algorithm.

Performance. ECC is known for its great performance, particularly in terms of computational efficiency and resource utilization. Compared to traditional public-key systems like RSA, ECC achieves the same level of security with much smaller key sizes, which translates into faster computation, reduced storage requirements, and lower power consumption.

Deployability. To make sure that our elliptic curves are not known too long in advance, or are precomputed in sufficient numbers, to mitigate preprocessing [12] as much as possible, we would need to generate the curves on the fly. While RSA groups only rely on the generation of sufficiently large prime numbers, ECC has an array of attacks to look out for as described in safecurves website and paper [7]. As such, generating a secure elliptic curve is a complex and challenging task. Nevertheless, there have been methods to generate efficiently safe elliptic curves ([8], 9, [10]) on the fly but these methods still necessitate minutes worth of probabilistic computation that is not easily verifiable. As finding the discrete logarithm of a number on a curve that has already been broken is significantly easier, thanks to the costly precomputation in Pollard’s Rho algorithm that can be reused (also succinctly mentioned in [10, attacking multiple keys]), we would have to regularly change the elliptic curve which would make ensuring their number is sufficiently large an important yet difficult challenge to solve.

Compliance. ECC is widely compliant with numerous industry standards and regulations, making it a trusted choice for modern cryptographic applications, including NIST guidelines, FIPS 186-4 and IETF standards for secure communication protocols. None of the methods, Index Calculus or Pollard’s $\rho$, are proprietary and there exists open source code implementing these.

3.2.3 Class group solutions

The class group of a number field is the group of fractional ideals modulo principal ideals, whose security is partially determined by a parameter called a discriminant. Class group of binary quadratic forms [14] omits trusted setup as the group order, also called class number, is believed to be difficult to compute when the discriminant is sufficiently large - more particularly the class number grows linearly to the square root of the discriminant. For a class group to be secure, the group size and discriminant must be sufficiently long - respectively at least 1,900 and 3,800 bit-long for 128 bit of security [4]- negative, square free and congruent to 0 or 1 modulo 4. Similarly to ECC, to break a class group security one has to find a class group discrete logarithm (CDLP) which can be done most efficiently with index calculus algorithms that reduce CDLP to integer factorization in sub-exponential time [5].

3.2.3.1 Design

Similarly to previous solutions, class groups present two types of problems satisfying the requirements: breaking the discrete logarithm by finding the class order, or using verifiable delayed functions. CDLP. In that case, the setup consists in generating a discriminant and generator $G$, and sampling a random point P from its secure subgroup. The challengers then have to find the scalar a such that $P = a \cdot G$. Verification is also straightforward, as it consists in raising $G$ to the power $a$ and verifying it equals $P$. The most efficient methods to find this scalar include the Index Calculus algorithm. VDF. Similarly to the CLPD, we first start by generating a discriminant and sample a random group element $G$. The challenge then consists in raising this element to a big exponent of the form $2^T$ where $T$ is set depending on the difficulty, the computation or time we want the challenger to need to solve the problem. The challengers eventually compute and output $y = x^{2^T} (\text{mod} N)$ by squaring the integer $x$ exactly $T$ times as well as generate an additional proof of this result. The verification consists in verifying the proof passes successfully together with the input, output and modulus.

3.2.3.2 Properties

Security Strength & Maturity. Class group-based cryptography has reached a moderate level of maturity in cryptographic research. While not as widely deployed as more traditional cryptographic methods like RSA or ECC, class group cryptography has gained attention due to its potential resistance to quantum computing attacks. The mathematical foundations, particularly the hardness of the class group discrete logarithm problem, are well-understood, and class group cryptosystems have been rigorously analyzed. However, practical deployment is still in the early stages, with ongoing efforts focused on optimizing efficiency, key management, and standardization.

Performance. Class group-based cryptography is generally less efficient than RSA or ECC due to the size of their elements and the computational complexity of the composition of elements. More particularly, to achieve strong security, class groups’ discriminants must be several thousands bit long, and group elements half of this. Operations are thus costly, especially as composition in class groups rely on finding the greatest common denominator between such numbers that is particularly expensive.

Deployability. Setting up class groups, even though their order is hidden, is much easier than previously discussed solutions as it consists in practice to generate a sufficiently long negative square-free random integer d, and such that d ≡ 1 mod 4. as discriminant. Generating a random element in a class group by hashing also is however more of a delicate but still feasible task as mentioned in [11]. Mysten Labs recently iterated on this work and published a more efficient and secure hash function [38] to class groups. Interestingly, there exist algorithms that have been designed to reuse the underlying group such as cascaded and continuous VDFs [13].

Compliance. Since class group-based cryptography is still being researched, it is not as broadly standardized or regulated as more established cryptographic techniques like ECC. That said, once formal standards and guidelines are developed and adopted, class group-based cryptography could achieve compliance with relevant legal and regulatory frameworks. None of the VDF proof generation algorithms are proprietary and there exists open source code implementing these. Other groups We mostly focused on commonly used groups, such as RSA and ECC, and class groups whose usage have been increasing lately, notably because of the popularity of VDF primitives. There exist however other groups such as lattices which are one of the main candidates for post quantum cryptography, supersingular isogenies, whose security is dubious at the moment since the attack on SIDH in 2022, and hyperelliptic Jacobians groups, which are still novel and need further time to get confidence in their security and for more protocols to be built upon, to cite a few.

3.2.4 OWF solutions

To widen our spectrum of solutions, we are now exploring solutions based on well-established non-trapdoored cryptographic functions and pair them with efficient proof systems to enable fast verification. Hash-based approaches are generally more cost-effective than asymmetric cryptography, do not depend on potentially vulnerable trapdoors, and can be implemented using widely deployed primitives. They are well understood both cryptographically and economically, especially given the prevalence of hash farms. The main drawback of hash functions lies in their verification: traditionally, verification requires recomputing the hashes, which can be too time-consuming for our use case, especially when considering synching. To address this, we propose leveraging proof systems, such as Succinct Non-interactive Arguments of Knowledge (SNARKs) and Scalable Transparent ARguments of Knowledge (STARKs) to reduce verification time. This introduces a modest overhead in the form of small proof sizes—on the order of hundreds of bytes—which remains acceptable. Although SNARKs are relatively new and involve complex protocols, their adoption is growing, with some blockchains like Mina and Midnight fully built around them. While their use may raise concerns, it remains a practical choice. It is worth noting, however, that SNARKs are not quantum-resistant—unlike their hash-based counterpart, STARKs, which do offer quantum resistance.

3.2.4.1 Proofs of knowledge

Proofs of knowledge have become an especially active and dynamic area of research in recent years. The foundations were laid in the 1990s with key contributions such as Bellare et al.'s work on Probabilistically Checkable Proofs (PCPs, [18]), Kilian’s results on interactive arguments of knowledge derived from PCPs [[17]], and Micali’s introduction of Computationally Sound Proofs (CS Proofs [16]), which transformed interactive proofs into non-interactive ones using the Fiat-Shamir heuristic. In 2016, Groth introduced one of the most efficient PCP-based proof systems to date [15], offering significant improvements in both verification time and proof size. Its main drawback, however, is its reliance on a lengthy trusted setup that cannot be reused across different applications. Subsequent advancements built on this foundation, with SNARKs compiling from interactive oracle proofs (IOPs) and polynomial commitment schemes (PCs) such as Plonk [19] and Marlin [20]. Researchers introduced novel techniques to optimize proving time—either by reducing asymptotic complexity, such as replacing FFTs with multivariate polynomials, or by enhancing circuit efficiency through the use of lookup tables [23], custom gates [24], and cryptographic primitives tailored for specific applications. More recently, proof aggregation has emerged as a promising paradigm. Techniques like folding and recursive proofs—exemplified by concepts such as Proof-Carrying Data (PCD, [21]) and Incrementally Verifiable Computation (IVC, [22])—enable efficient step-by-step computation and verification. Despite ongoing debates about their security—particularly around the soundness of modeling a random oracle (RO) inside a SNARK—these systems are increasingly being integrated into blockchain technologies. Projects like ZCash, Mina, and Midnight blockchains leverage SNARKs for their powerful compression capabilities, and in some cases, for their privacy-preserving features as well.

3.2.4.2 OWFs

Non-Algebraic standard hashes. SHA-2, SHA-3, and BLAKE2 are prominent cryptographic hash functions widely used today. SHA-2, standardized by NIST in 2001, remains the industry standard due to its strong security and broad adoption in applications like TLS and cryptocurrencies. Keccak [25], selected through a NIST competition in 2015 as the new standard SHA-3, offers a fundamentally different sponge-based design, providing an alternative with enhanced flexibility and resilience at the cost of lower throughput. BLAKE2 [[26]], developed as a high-performance finalist in the same SHA-3 competition, is favored for its speed and security, often outperforming both SHA-2 and SHA-3 in practical settings. While not standardized by NIST, BLAKE2 is widely trusted and increasingly adopted in modern cryptographic implementations. Together, these functions represent a balance of security, performance, and diversity in cryptographic hashing today.

While these hash functions are very efficient on CPU, they are very expensive to verify with classic SNARKs, as the latter are working on prime fields and not bits. Proving hash evaluation is several orders of magnitude higher than evaluating on CPU making this solution very impractical. Simple benchmarks demonstrate such results, with the generation of a proof asserting the evaluation of a few hundreds of hashes taking tens of seconds, while the evaluation itself is of the order of the microsecond. For instance, according to Figure 1, the a hundred evaluations of SHA-256 would take 32μs on CPU and require 300,000 gates. To generate a proof of these evaluations, we would require a circuit of size 219 , i.e. the smallest power of 2 above 300,000, which takes 6s to 18s depending on the commitment scheme, making this solution, combining standard hash functions and SNARKs, highly impractical.

Figure 1, taken from Reinforced Concrete paper [27]. Performance of various hash functions in the zero knowledge (preimage proof) and native (hashing 512 bits of data) settings on Intel i7-4790 CPU (3.6 GHz base frequency, 4 core, 8 threads).

$\text{log}_2(\text{gates})$	#gates	Proving time - KZG (ms)	Proving time - IPA (ms)
$8$	256	43	77
$9$	512	58	105
$10$	1,024	75	153
$11$	2,048	100	210
$12$	4,096	157	330
$13$	8,192	218	500
$14$	16,384	342	856
$15$	32,768	540	1,432
$16$	65,536	917	2,590
$17$	131,072	1,646	4,779
$18$	262,144	3,028	9,199
$19$	524,288	6,231	18,496
$20$	1,048,576	12,743	37,287

Table 2. Halo2 benchmarks, using KZG [28] and IPA [29] commitment schemes on Intel(R) Core(TM) i9-14900HX (2.2 GHz base frequency, 24 cores, 32 threads).

Memory-hard functions (MHFs). are primitives relying on hash functions designed to resist attacks by requiring significant memory and computational effort, making them particularly interesting in our use case, where memory would become another bottleneck to an adversary attempting a grinding attack. Argon2, the winner of the Password Hashing Competition in 2015, is the current industry standard due to its strong security, configurability, and resistance to known attacks. Balloon Hashing offers a simpler design focused on provable security guarantees and ease of analysis but is less widely adopted. The MHF scrypt, introduced earlier and used notably in cryptocurrencies like Litecoin, was among the first practical memory-hard functions but has seen some theoretical attacks exploiting trade-offs between memory and computation. Of the three, only Argon2 is formally standardized in RFC 9106 and recommended for new applications, while scrypt remains popular in legacy systems and Balloon Hashing is still primarily academic. Unfortunately, these primitives are much more expensive than hashes on CPU as well as on SNARKs, where the memory requirements become even more prohibitive.

SNARK-friendly hashes. A novel branch of research started with the adoption of SNARKs to design SNARK friendly hash functions. We can classify them in two categories: algebraic or not. Algebraic hashes include, but are not limited to, Poseidon [30], Anemoi [31], Rescue [32] which are based on prime fields. Choosing carefully the fields can result in optimizations of 2 to 3 orders of magnitude in SNARKs, but with higher CPU time unfortunately. For instance, a hundred evaluations of Poseidon hash would take 1.9ms, compared to 32μs for SHA-256, on CPU, but the proof generation would take 1s to 3s, compared to 6s to 18s for SHA-256. Other, non algebraic, hash functions have also been created such as Reinforced Concrete [27] and Monolith [33] to minimize the cost of binary operations by making the most of lookup tables, which store binary operations on vectors of bits. The fact that these hash functions are less efficient on CPUs is not problematic as we are only interested in computational cost. Unfortunately, the ratio between CPU and prove generation time still remains too high for our usage. More novel techniques in SNARKs, such as IVC or folding, would be needed to make the “snarkification” of hash practical but these progresses have yet to reach maturity, be it in both theory and practice. Another caveat to using SNARK-friendly hashes would be that adversaries could afford specialised hardware such as CPUs with special instructions such as AVX2, or GPUs, FPGAs or ASICs to accelerate prime field operations and widen the gap between honest users and adversaries.

3.2.4.3 Design

Using OWFs and SNARKs in the context of Phalanx is straightforward. To each iteration is associated a input that we have to recursively hash a number of times set by the total duration and number of iterations with the desired primitive. Once the result is computed, a SNARK proof can be generated proving the correctness of the computation. We can remark that IVC based solutions are particularly adapted as a choice for SNARK primitves as we can prove a batch of iterations per step of IVC. Both the hash output and the SNARK are then published.

3.2.4.4 Properties

Security Strength & Maturity. While traditional hashes have strong security, more novel ones, especially the more usable with SNARKs, can be deemed too novel for adoption. SNARKs, and SNARKs friendly primitives, are very complex pieces of technology that have been broken before and are still evolving at a rapid pace. SNARKs are not postquantum resistant but STARKs are.

Performance. While hash functions are extremely efficient on commodity hardware, the proof generation with current SNARKs is far too slow for this solution to be practical

Deployability. SNARKs are difficult to deploy, they rely on different libraries that are not easy to update. Changing of SNARKs is also tedious as circuits would very likely need to be rewritten, adding further risk and complexity.

Compliance. Hash functions are standardized and libraries are easily available. SNARK solutions are not copyrighted, there is however a limited number of available libraries, which can either be open source or proprietary (SP1, RISC0, STARKNET…).

3.3 Primitive recommendation

The combination of OWFs and SNARKs, however elegant it may be for its modularity, is not practical for the proof generation overhead being prohibitive. Trapdoor based solutions seem to be the best candidates for anti-grinding solutions. Out of the ones considered, VDFs seem the most practical primitive thanks to the possibility of reusing the group, and class groups offer the simplest deployment. The main caveat of such a solution is in its relative novelty, regular assessment would need to be done to ensure correct and up to date parametrization.

Path to Active

Acceptance Criteria

The proposal will be considered Active once the following criteria are met:

• The revised cardano-node implementation passes all node-level conformance test suites.
• A formal security audit is completed and its findings reviewed.
• The solution demonstrates stable and expected behavior in testnet environments.
• The hard fork is successfully executed and the protocol transition is secure.
• The community agrees on the initial Phalanx protocol parameters and on a clear policy for their future updates.
• The upcoming CIP introducing a Consensus category may define further acceptance criteria, which will be incorporated accordingly.

Implementation Plan

To fulfill the above criteria, the following steps are planned:

• Triage and scope confirmation by Intersect’s Core Infrastructure and Consensus teams.

• Coordination with ongoing workstreams on consensus protocol enhancements:

  • Compatibility with Peras
  • Compatibility with Leios
  • Compatibility with Ouroboros Genesis

• Development and publication of a community communication plan covering:

  • The initial values of Phalanx parameters
  • The procedure for evaluating and updating these parameters

• Integration of a Wesolowski-style VDF library into cardano-crypto-class

• Implementation of the node-level logic, including support for the hard fork mechanism

• Construction and execution of a comprehensive node-level conformance test suite

References

1. Ouroboros Randomness Generation Sub-Protocol – The Coin-Flipping Problem
2. Cardano Disaster Recovery Plan
3. Baigneres, Thomas, et al. "Trap Me If You Can--Million Dollar Curve." Cryptology ePrint Archive (2015).
4. Lenstra, Arjen K., et al. "The number field sieve." Proceedings of the twenty-second annual ACM symposium on Theory of computing. 1990.
5. National Institute of Standards and Technology (NIST). (April 2010). Special Publication 800-78-5: Cryptographic Algorithms and Key Sizes for Personal Identity Verification.
6. Dobson, Samuel, Steven Galbraith, and Benjamin Smith. "Trustless unknown-order groups." arXiv preprint arXiv:2211.16128 (2022).
7. Hamdy, Safuat, and Bodo Möller. "Security of cryptosystems based on class groups of imaginary quadratic orders." Advances in Cryptology—ASIACRYPT 2000: 6th International Conference on the Theory and Application of Cryptology and Information Security Kyoto, Japan, December 3–7, 2000 Proceedings 6. Springer Berlin Heidelberg, 2000.
8. Boneh, Dan, et al. "Verifiable delay functions." Annual international cryptology conference. Cham: Springer International Publishing, 2018.
9. Bernstein, Daniel J., and Tanja Lange. "Safe curves for elliptic-curve cryptography." Cryptology ePrint Archive (2024).
10. Baier, Harald. Efficient algorithms for generating elliptic curves over finite fields suitable for use in cryptography. Diss. Technische Universität, 2002.
11. Konstantinou, Elisavet, et al. "On the efficient generation of prime-order elliptic curves." Journal of cryptology 23.3 (2010): 477-503.
12. Miele, Andrea, and Arjen K. Lenstra. "Efficient ephemeral elliptic curve cryptographic keys." Information Security: 18th International Conference, ISC 2015, Trondheim, Norway, September 9-11, 2015, Proceedings 18. Springer International Publishing, 2015.
13. Seres, István András, Péter Burcsi, and Péter Kutas. "How (not) to hash into class groups of imaginary quadratic fields?." Cryptographers’ Track at the RSA Conference. Cham: Springer Nature Switzerland, 2025.
14. Corrigan-Gibbs, Henry, and Dmitry Kogan. "The discrete-logarithm problem with preprocessing." Advances in Cryptology–EUROCRYPT 2018: 37th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tel Aviv, Israel, April 29-May 3, 2018 Proceedings, Part II 37. Springer International Publishing, 2018.
15. Ephraim, Naomi, et al. "Continuous verifiable delay functions." Annual International Conference on the Theory and Applications of Cryptographic Techniques. Cham: Springer International Publishing, 2020.
16. Long, Lipa. "Binary quadratic forms.", (2018)
17. Groth, Jens. "On the size of pairing-based non-interactive arguments." Advances in Cryptology–EUROCRYPT 2016: 35th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Vienna, Austria, May 8-12, 2016, Proceedings, Part II 35. Springer Berlin Heidelberg, 2016.
18. Micali, Silvio. "CS proofs." Proceedings 35th Annual Symposium on Foundations of Computer Science. IEEE, 1994
19. Kilian, Joe. "A note on efficient zero-knowledge proofs and arguments." Proceedings of the twenty-fourth annual ACM symposium on Theory of computing. 1992.
20. Bellare, Mihir, et al. "Efficient probabilistically checkable proofs and applications to approximations." Proceedings of the twenty-fifth annual ACM symposium on Theory of computing. 1993.
21. Gabizon, Ariel, Zachary J. Williamson, and Oana Ciobotaru. "Plonk: Permutations over lagrange-bases for oecumenical noninteractive arguments of knowledge." Cryptology ePrint Archive (2019).
22. Chiesa, Alessandro, et al. "Marlin: Preprocessing zkSNARKs with universal and updatable SRS." Advances in Cryptology–EUROCRYPT 2020: 39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, May 10–14, 2020, Proceedings, Part I 39. Springer International Publishing, 2020.
23. Bitansky, Nir, et al. "Recursive composition and bootstrapping for SNARKS and proof-carrying data." Proceedings of the forty-fifth annual ACM symposium on Theory of computing. 2013.
24. Valiant, Paul. "Incrementally verifiable computation or proofs of knowledge imply time/space efficiency." Theory of Cryptography: Fifth Theory of Cryptography Conference, TCC 2008, New York, USA, March 19-21, 2008. Proceedings 5. Springer Berlin Heidelberg, 2008.
25. Gabizon, Ariel, and Zachary J. Williamson. "plookup: A simplified polynomial protocol for lookup tables." Cryptology ePrint Archive (2020).
26. Gabizon, Ariel, and Zachary J. Williamson. "Proposal: The turbo-plonk program syntax for specifying snark programs.", 2020
27. Bertoni, Guido, et al. "Keccak." Annual international conference on the theory and applications of cryptographic techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013.
28. Aumasson, Jean-Philippe, et al. "BLAKE2: simpler, smaller, fast as MD5." International Conference on Applied Cryptography and Network Security. Berlin, Heidelberg: Springer Berlin Heidelberg, 2013.
29. Grassi, Lorenzo, et al. "Reinforced concrete: A fast hash function for verifiable computation." Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security. 2022.
30. Kate, Aniket, Gregory M. Zaverucha, and Ian Goldberg. "Constant-size commitments to polynomials and their applications." International conference on the theory and application of cryptology and information security. Berlin, Heidelberg: Springer Berlin Heidelberg, 2010.
31. Bünz, Benedikt, et al. "Bulletproofs: Short proofs for confidential transactions and more." 2018 IEEE symposium on security and privacy (SP). IEEE, 2018.
32. Grassi, Lorenzo, et al. "Poseidon: A new hash function for {Zero-Knowledge} proof systems." 30th USENIX Security Symposium (USENIX Security 21). 2021.
33. Bouvier, Clémence, et al. "New design techniques for efficient arithmetization-oriented hash functions: Anemoi permutations and Jive compression mode." Annual International Cryptology Conference. Cham: Springer Nature Switzerland, 2023.
34. Szepieniec, Alan, Tomer Ashur, and Siemen Dhooghe. "Rescue-prime: a standard specification (SoK)." Cryptology ePrint Archive (2020).
35. Grassi, Lorenzo, et al. "Monolith: Circuit-friendly hash functions with new nonlinear layers for fast and constant-time implementations." IACR Transactions on Symmetric Cryptology 2024.3 (2024): 44-83.
36. Wesolowski, Benjamin. "Efficient verifiable delay functions." Advances in Cryptology–EUROCRYPT 2019: 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, May 19–23, 2019, Proceedings, Part III 38. Springer International Publishing, 2019.
37. Pietrzak, Krzysztof. "Simple verifiable delay functions." 10th innovations in theoretical computer science conference (itcs 2019). Schloss Dagstuhl–Leibniz-Zentrum für Informatik, 2019.
38. Chalkias, Kostas Kryptos, Jonas Lindstrøm, and Arnab Roy. "An efficient hash function for imaginary class groups." Cryptology ePrint Archive (2024).

Copyright

This CIP is licensed under Apache-2.0.

Portions of this document were prepared with the assistance of AI-based tools.The use of AI was limited to drafting, editing, and improving clarity of expression. All technical ideas, specifications, and cryptographic designs originate from the human authors, who take full responsibility for their novelty, correctness, and originality.

The AI contribution is comparable to that of a copy-editor: it helped improve formatting, emphasis, and readability, but did not generate or propose the underlying concepts.